前回は「補助線を発見する考え方・コツ・ポイント〜図形の線を消してみる発想・「出っぱった図形を整理」する発想・整理する発想と解き方・変わったポイントと「解く鍵」〜」の話でした。
応用問題が「難しい」とき：基礎と応用の間に立ちはだかる「高い壁」
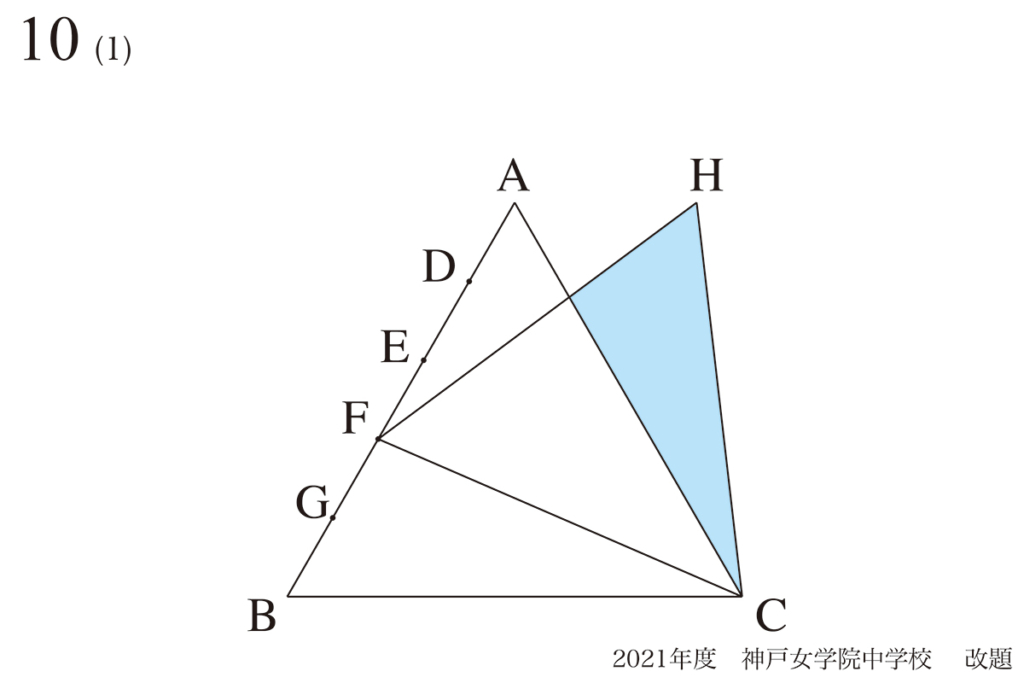
今回は、算数の基本的問題がある程度出来るようになってから、応用問題攻略の話です。
旅人算・ニュートン算・流水算・方陣算・図形・・・・・と算数は多数の分野があります。
男子小学生旅人算の基本的な
問題は出来るけど・・・
男子小学生色々な人が出てきて、
複雑になると分からない・・・
女子小学生図形問題は、基本的なことは
大体マスターしたけど・・・
女子小学生ちょっと難しい問題になると、
補助線が上手く見つけられない・・・
ある程度の問題が解けるようになったのに、「応用問題になると解けない」と悩むのが算数です。
この「応用問題が難しい」のは、各科目共通です。
共通ですが、「基本と応用」の間に「立ちはだかる高い壁」が最も高く感じられるのが算数です。
この「立ちはだかる高い壁」を前にすると、
男子小学生はあ・・・
こういう問題沢山できるようにならないと・・・
女子小学生この問題集全部
出来るようにならないと・・・
「立ちはだかる高い壁」がたくさんあって、まるで山脈のように壁が連なっているように感じます。
男子小学生この「高い壁」を
少しずつ全部乗り越えないと・・・
女子小学生頑張って、どんどん
勉強しないと・・・
たくさんの分野と科目を勉強しなければならない、中学受験生は大変です。
「共通する考え方」と「考え方の軸」を学ぶ発想
難しく感じてしまい、「歯が立たない」とすら思えてしまうことがある算数の応用問題。
理科・社会・国語は「応用問題になったら全く出来ない」ということは、あまりありません。
応用問題は難しいですが、
男子小学生ここまでは
出来たんだけどさ・・・
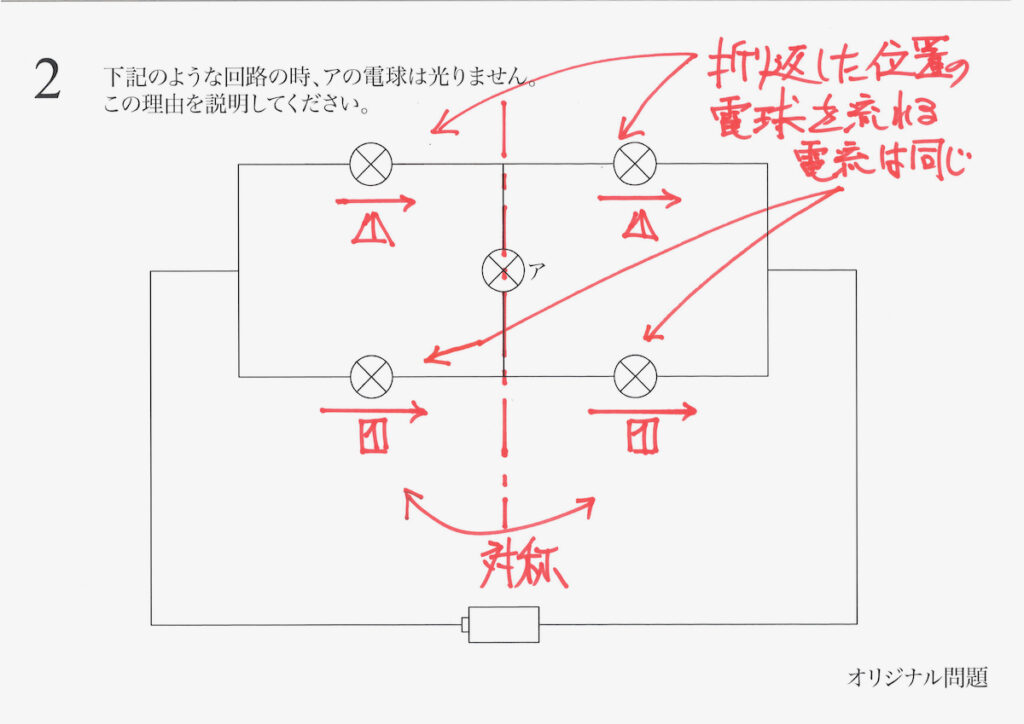
女子小学生この電気の問題は
難しいけど、最後の問題以外は出来た・・・
ある程度は出来る傾向があります。
対して、算数は応用問題になると、一気に難しく感じられる傾向があります。
男子小学生この算数の問題、
全然分からないんだけど・・・
女子小学生(1)から(3)まであるけど、
(1)も分からない・・・
例えば、「(1)から(3)まである大問」ならば「(1)は比較的易しい」傾向があります。
それなのに、「(1)すら出来ない」と、
女子小学生(3)まであるのに、(1)も
分からないのは、全然ダメなのかな・・・
誰しもテンションが下がってしまいます。
応用問題で「(1)から(3)まである大問の(1)は易しい方」が多いですが、大事なポイントがあります。
それは、「各問題の考え方には共通点がある」ことが多いことです。
そこで、
女子小学生(1)すら
出来ない・・・
このように「テンションが下がってしまう」のではなく、
女子小学生(1)から(3)は「共通する考え方」がある
はずだから、それを学ぼう！
このようにポジティブに「共通する考え方」を学びましょう。
・小問に分かれている場合は、「共通する考え方」をしっかり学ぶようにする
・良問をしっかり学んで、「考え方の軸」を吸収する
参考書・問題集・塾のテキストの多くは、様々な学校の過去問です。
中にはオリジナル問題もあるでしょうが、ほとんどは過去問でしょう。
それは、各校の過去問が「非常によく考えられている問題」だからです。
そして、応用問題を解くときは「考え方」や「考え方の軸」をよく理解して、吸収しましょう。
応用問題が解けるようになる勉強法：補助線と答えの関係性
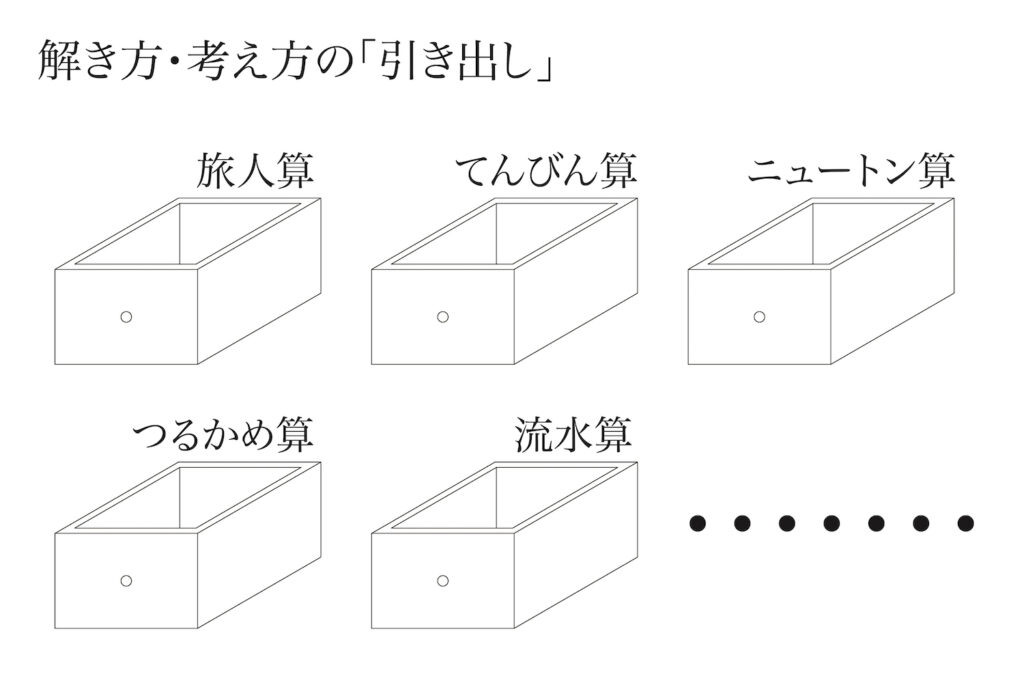
「小問に分かれている大問」の時は、ある共通する考え方や性質を繰り返し学ぶ良い機会です。
その時は、「たった一問」と考えずに「ある考え方を繰り返し学ぶチャンス」と考えましょう。
・ある共通する考え方や性質を繰り返し学ぶ
・応用問題を理解して、一つの引き出しをつくる
そして、その問題をしっかり理解することで、「一つの引き出し」をつくるようにしましょう。
そういう「考え方の引き出し」が少しずつ出来ると、学力が上がるでしょう。
この時「パターン暗記」や「解法パターンに分類」しないことが大事です。
「思考の軸」を構築してゆくイメージで、学んでみましょう。
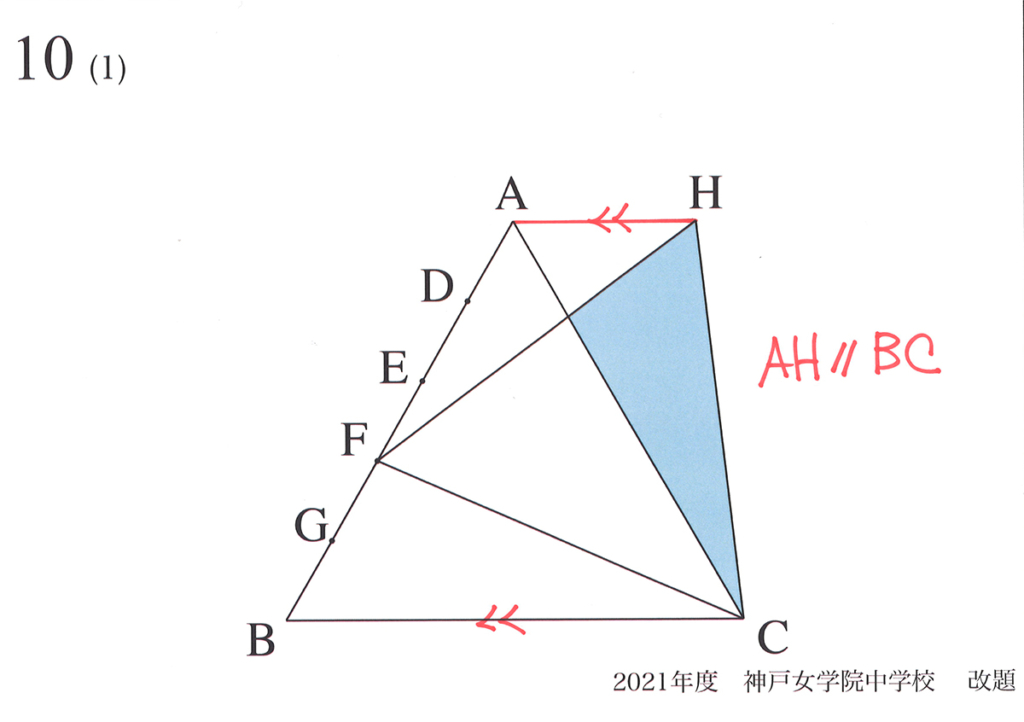
算数実践紀行で神戸女学院中学の正三角形の問題を取り上げました。
原題では「(1)と(2)」でしたが、筆者が「(3)と(4)を追加」した問題です。
正三角形の性質が分かり「動く点・動点」も学べる、とても良い問題です。（上記リンク）
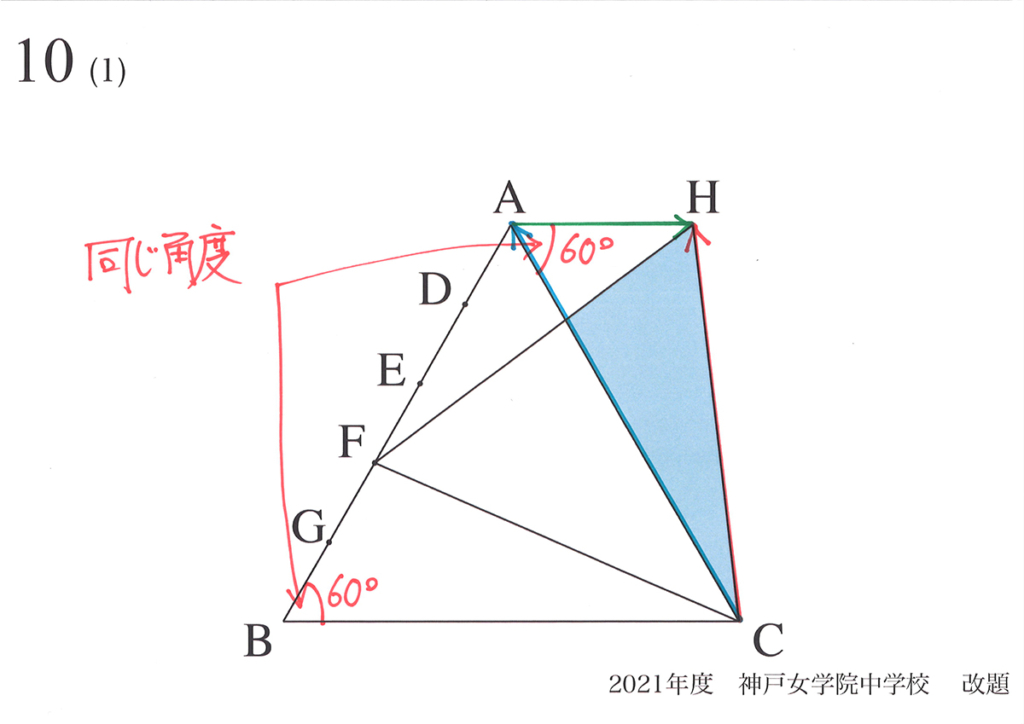
この「新たに正三角形が出来る」ことを考えるには「矢印を考える」のが最も良いです。
「矢印」は、中学・高校数学で学ぶベクトルの基本概念です。
小学生でも理解できるように、矢印の話を上記リンクでご紹介しています。
この「矢印の考え方」が「自分に合うかどうか」は、その方の学力や個性によります。
塾講師この問題は、
ここに補助線を引くと良い！
このように「良い補助線」を教わったところで、
男子小学生なぜ、ここに補助線を
引く発想が出るんだろう・・・
男子小学生算数のセンスや
ひらめきなのかな・・・
このように学ぶ側の子どもたちは「どうやって分かるの？」と思うでしょう。
ここで、補助線を考えるときに、
男子小学生なぜ、この補助線を
引くと「分かる」のだろう・・・
「なぜ、この補助線なのか？」を考えてみることは、とても良いです。
「なぜ？」ということを、ほんの少し考えて、
女子小学生この三角形の面積が
分かるには、何が分かれば良いのだろう・・・
「問題を解くために、何が分かりたいか」を考えるようにしましょう。
・「問題を解くために、何が分かりたいか」を考える
・その「分かりたい何か」を知るために、補助線などが「どう関係するか」を考える
図形問題であれば、「求めるべき答えと補助線の関係」を少し考えてみると良いでしょう。
すると、
女子小学生あ・・・
そういうことか・・・
ちょっとした「気づき」が生まれるでしょう。
この「ちょっとした気づき」の気づき方は、それぞれの方の個性や学力によると考えます。
この「関係を考える」は、少し難しく感じられる方もいるでしょう。
算数の学力のレベルによりますが、このように「なぜ、こう考えるか？」を考えること。
「なぜ、こう考えるか？」を積み重ねると、応用問題が解けるようになります。
そして、この姿勢は基本から応用へと展開する際に、最も大事な発想です。
次回は下記リンクです。
