前回は「回転移動する図形が「謎解き」のように楽しくなる姿勢〜まずは分かったことを整理・図形の外に線を延長・外の世界に出る発想問題・分析するように少しずつ解明・「謎解き」のように楽しい感覚・問題8(4)解法A〜」の話でした。
今回は(4)の解法Bです。
問題 8（再掲載）
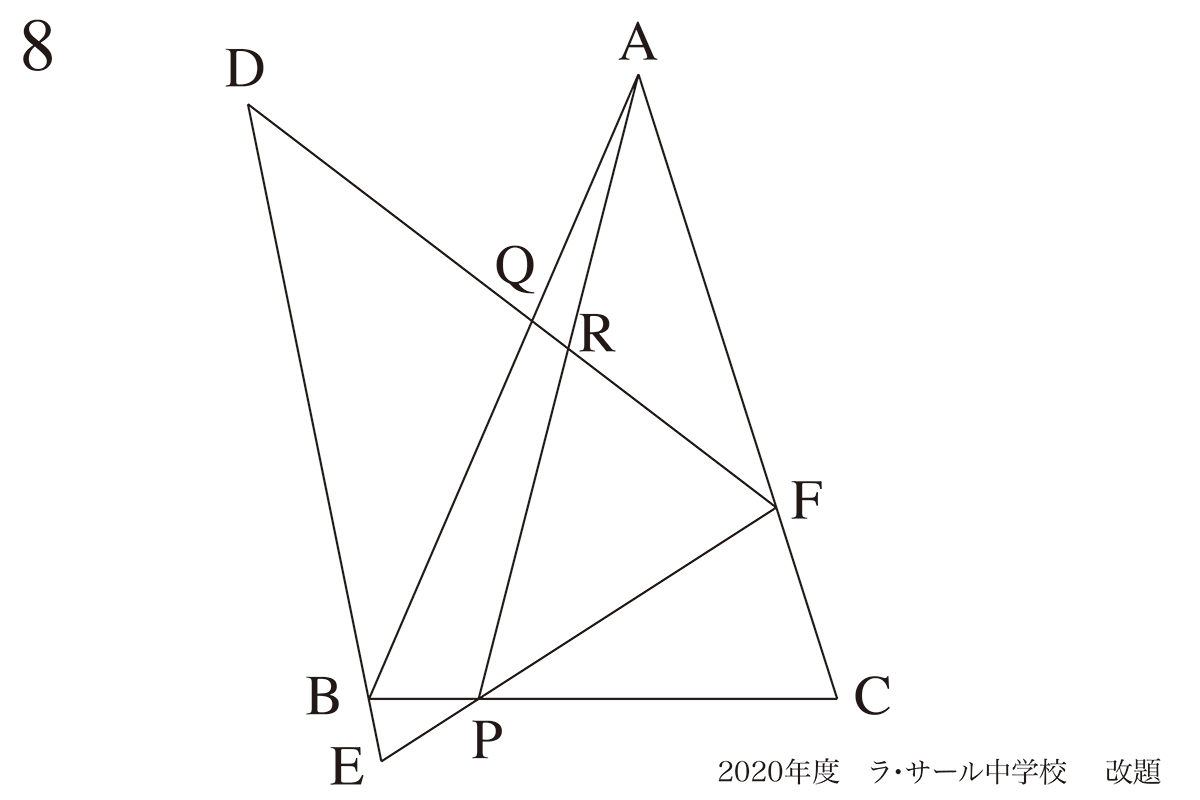
図形の中に新たに平行な線を引く：相似形を作り出す
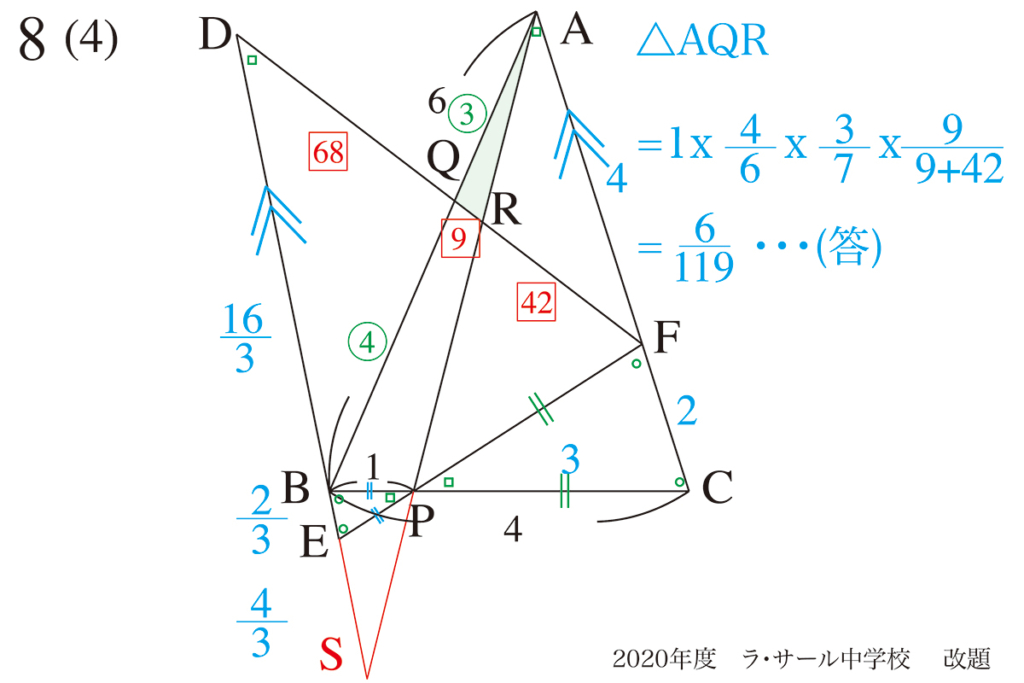
解法Aでは、「図形外に直線を延長して相似形を作る」考え方でした。
今回は、「図形の中で平行線（補助線）を引いて相似形を作る」考え方です。
・図形の外に平行な線を延長する
・図形の中に、新たに平行な線（補助線）を引く
解法Aと同様に、QR:RFを考えます。
別な相似三角形を作ってみましょう。
BCに並行な直線DT、UFを自分で作ってみましょう。
男子小学生平行な線を引くと、
相似形が出来るけど・・・
男子小学生DTは「新たな点T」が出てくるし、
UFも「新たな点U」が出てくる・・・
女子小学生新しい点がたくさん出てくると、
考えにくそうだけど・・・
相似形が作れれば「なんとかなる」姿勢
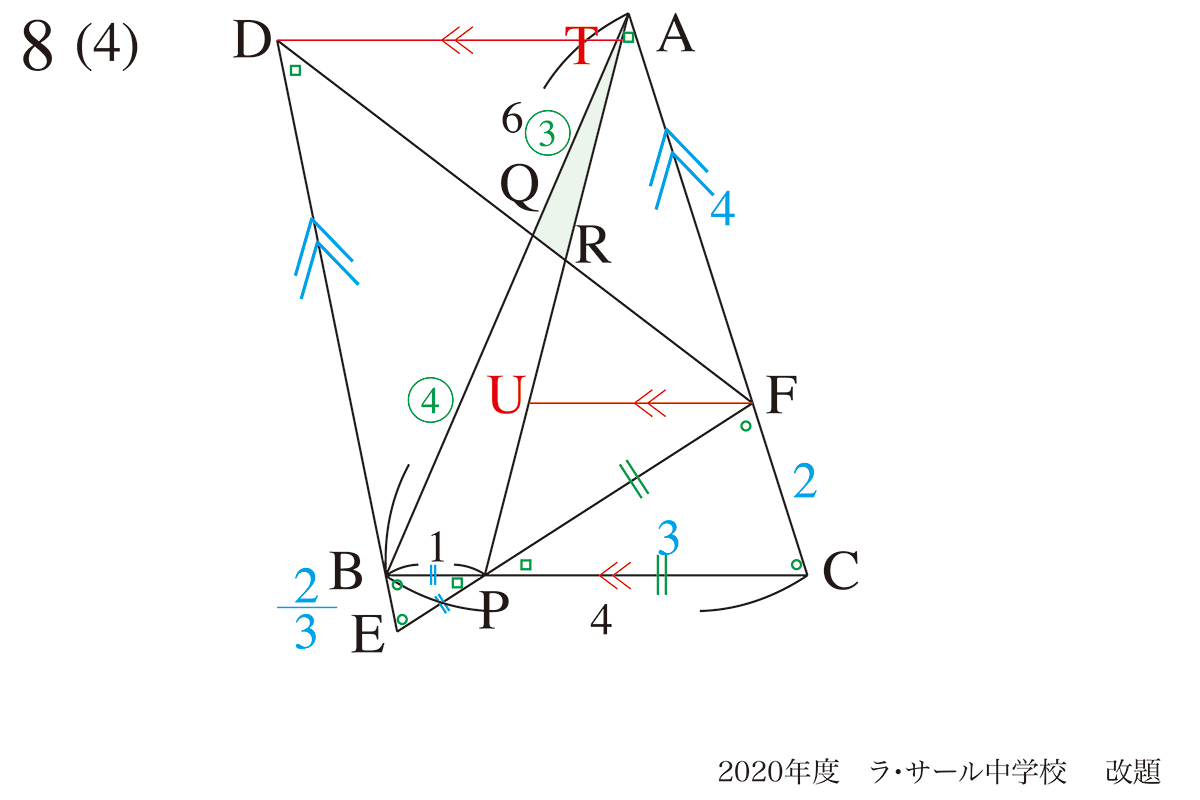
新たな点T、Uが登場しました。
そして、△RTDと△RUFが相似三角形です。
DF、APのように交差する直線に対して、平行な直線を新たに考えると良いでしょう。
すると、相似三角形が比較的簡単に作れます。
女子小学生確かに、新しい相似形が
出てきたけど・・・
女子小学生なんだか難しそうな
気がする・・・
図形問題では、「多少複雑になっても、相似形を地道に考えればなんとかなる」ことが多いです。
・相似形を探す
・平行な線を引いて、相似形を新たに作り出す
・相似形が見つかれば、「なんとか解くことが出来る」と考える
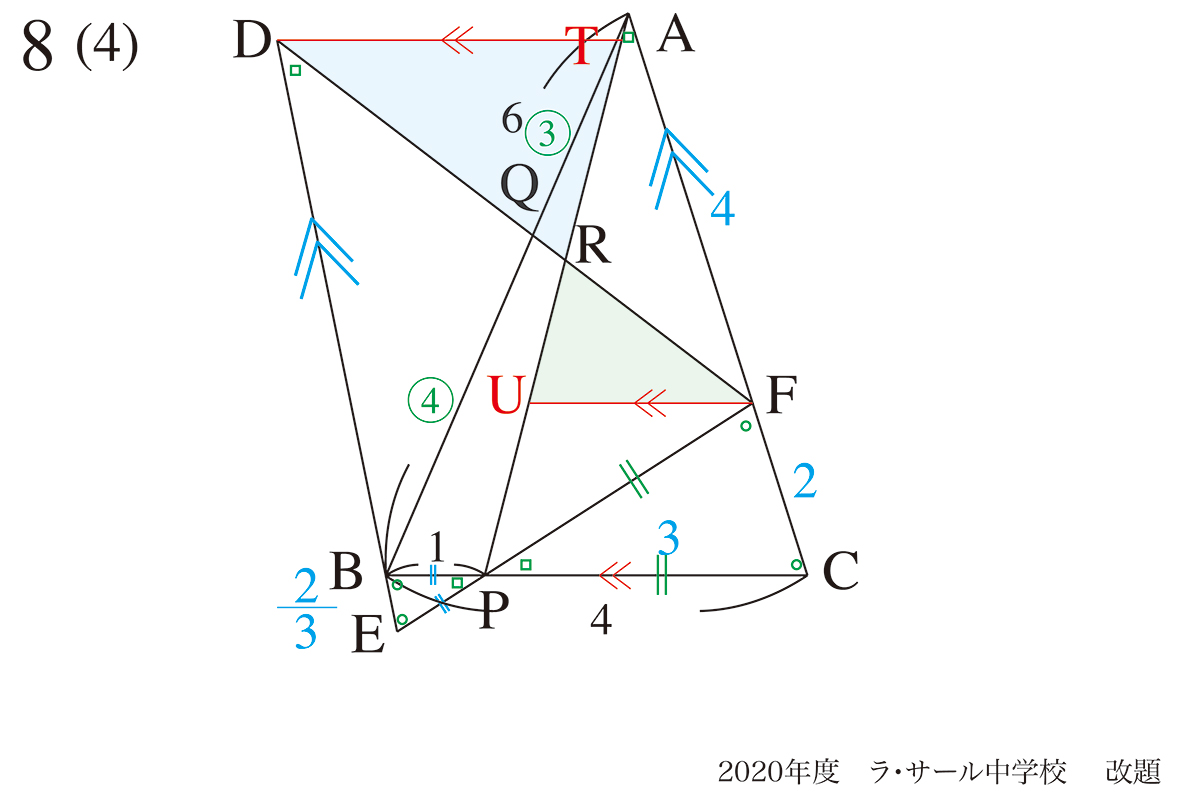
これらの相似比を利用して、QR:RFを求めたいです。
DT、UFは自分で設定した直線ですから、長さがわかりません。
男子小学生これでは、
先に進まないけど・・・
分からないなら、自分で考えて求めましょう。
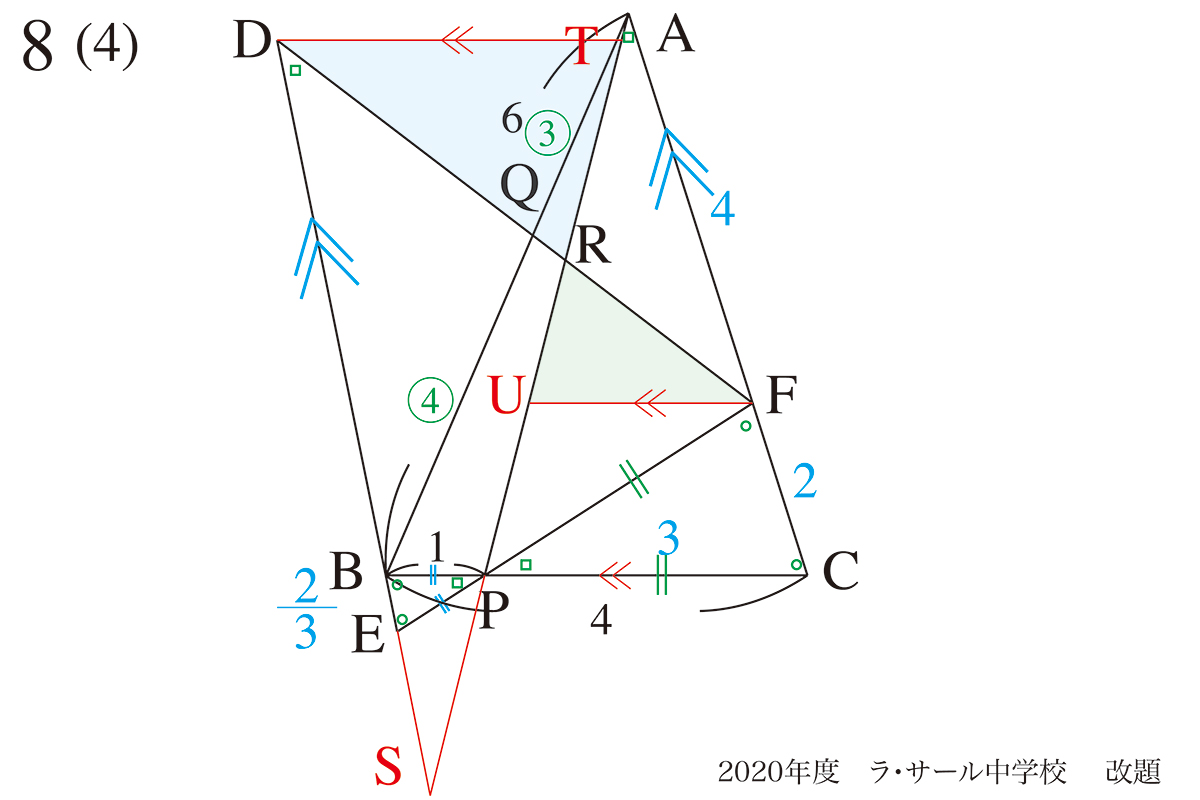
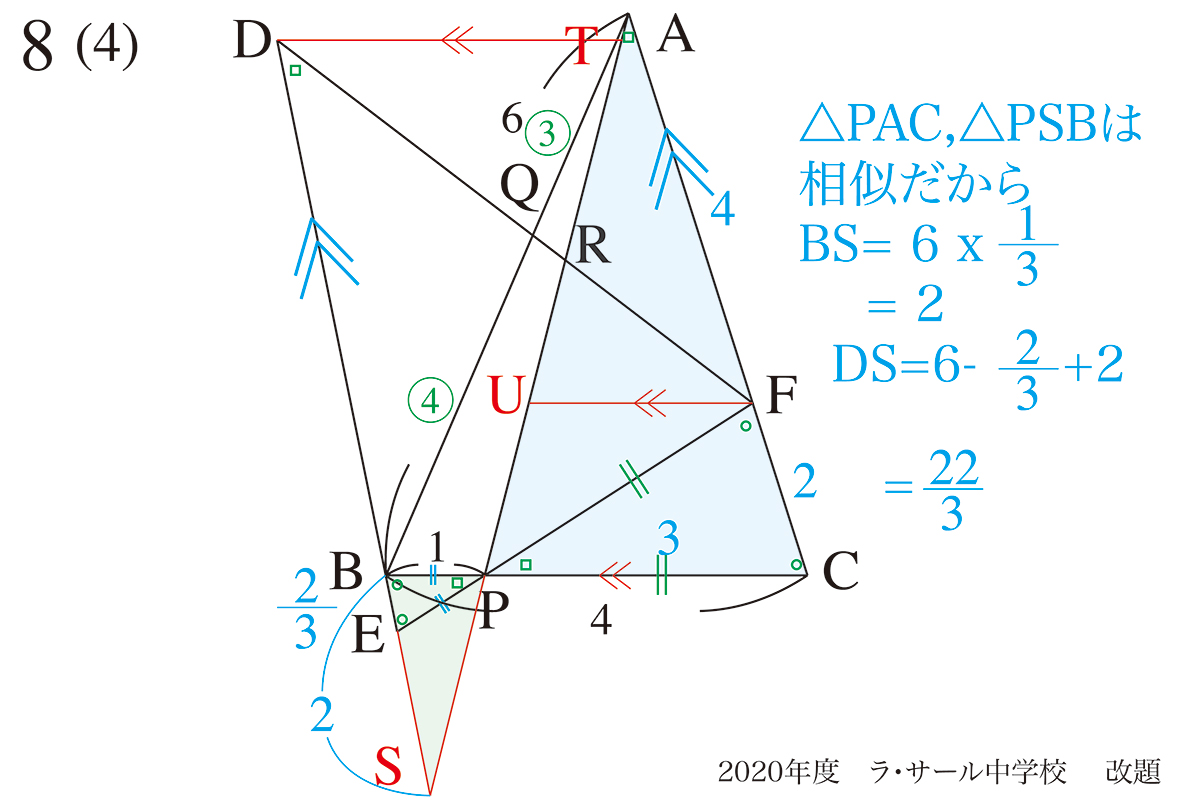
まずは、△SBPと△SDTの相似関係を使うために、BSとDSの長さを求めます。
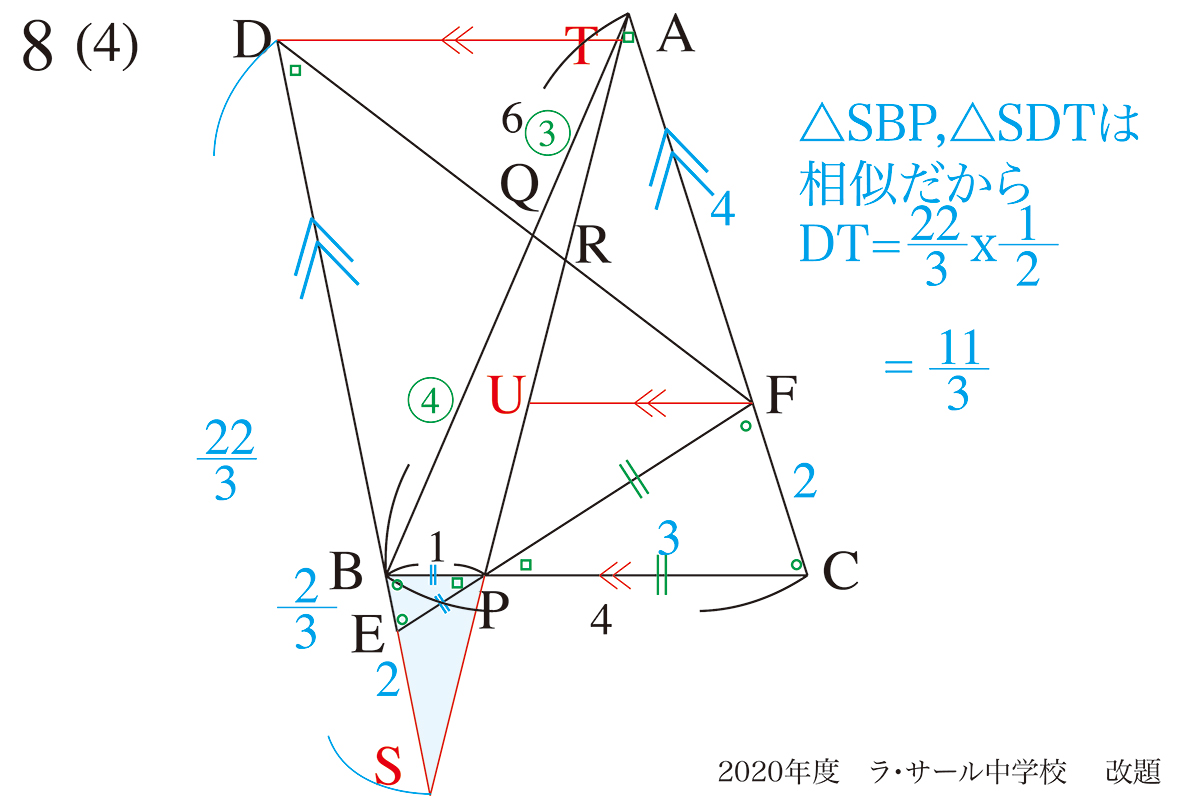
△SBPと△SDTの掃除関係から、DTの長さが求まります。
男子小学生確かに、少しずつ
「分からない長さ」が分かってくるね・・・
もう少しです。
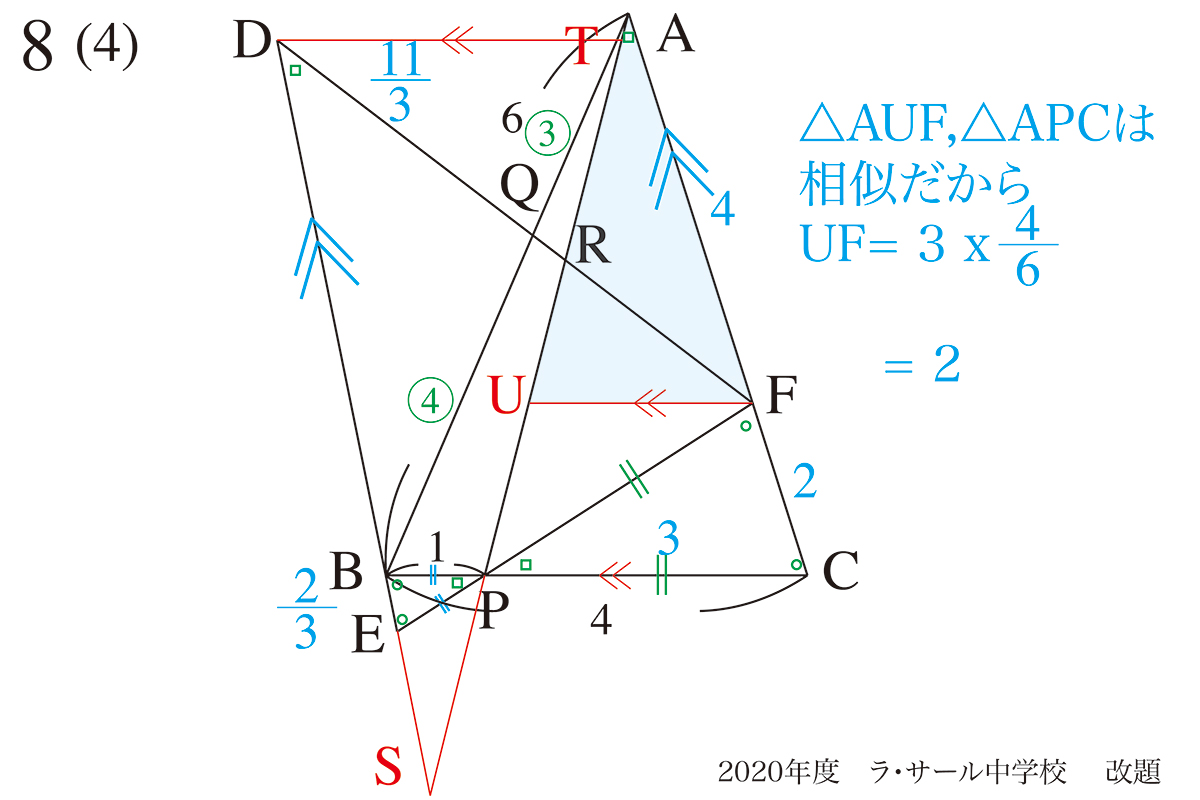
次に△AUFと△APCの相似関係から、UFの長さが求まります。
元の△ABCなどの二等辺三角形は「斜辺:底辺= 2 : 1 」なので、UF=AFx1/2と考えても良いです。
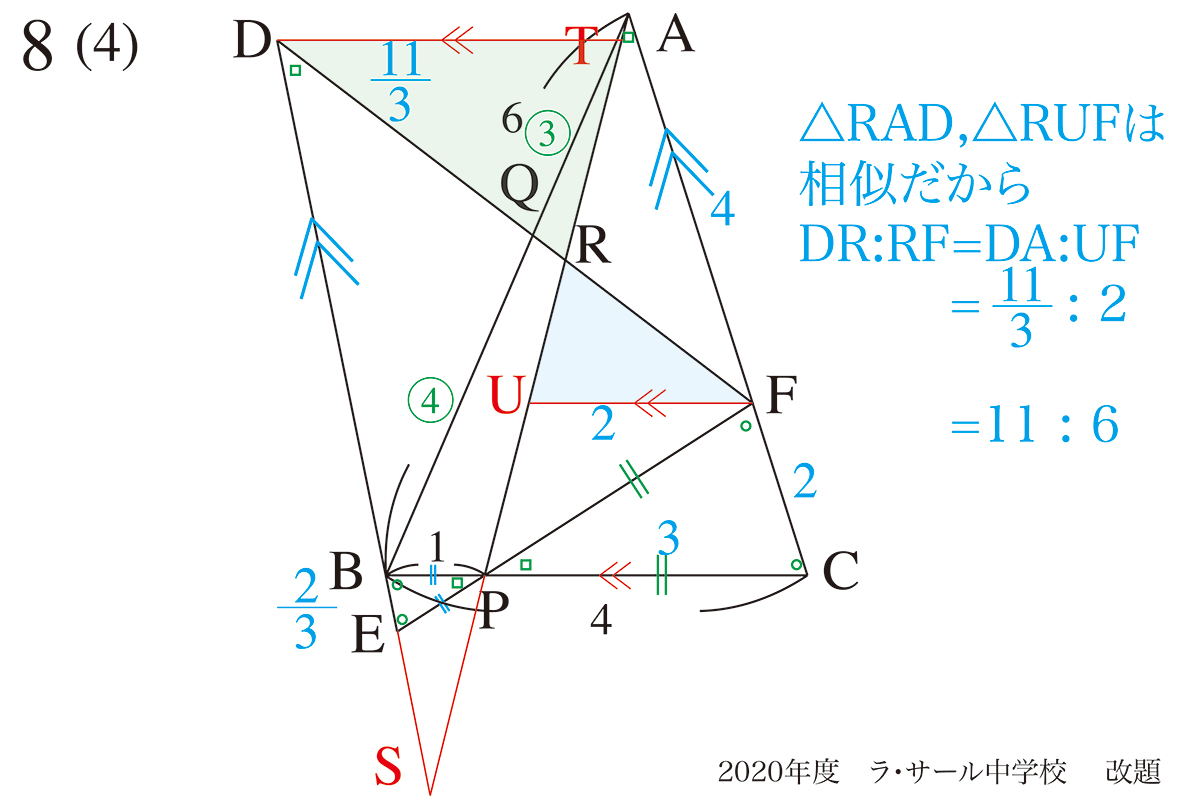
これで、やっとDR:RFの比が求まりました。
女子小学生ちょっと大変だったけど、
なんとか出来たね！
ここから先は解法Aと同じですので、省略します。
図形の発想を磨く：自分で補助線を引いて試行錯誤
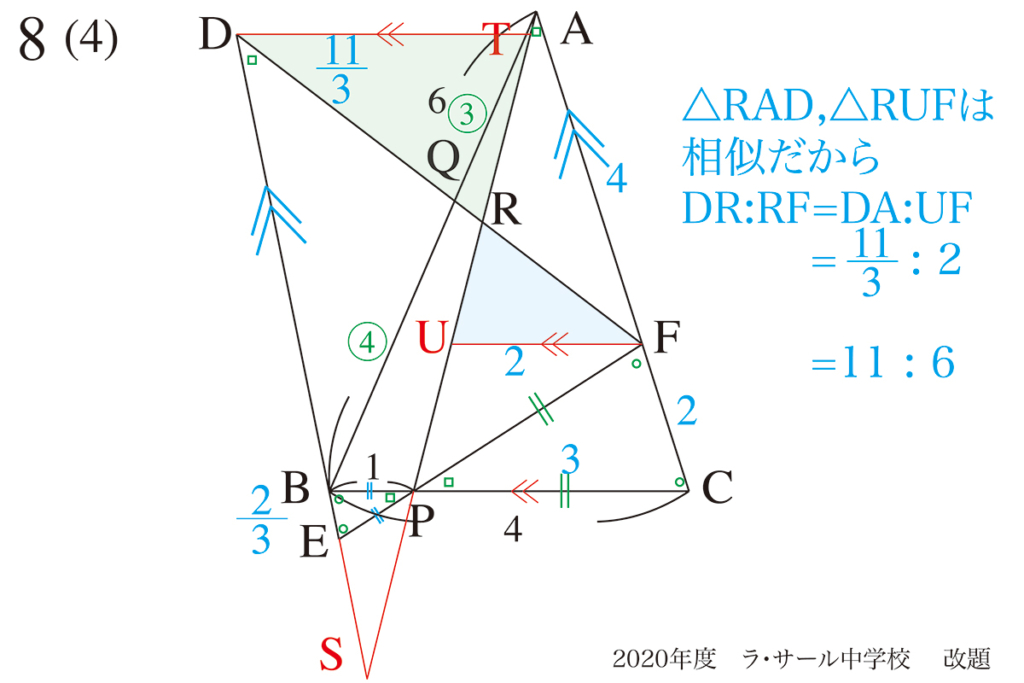
解法Aの方が素直で、解法Bは少し遠回りです。
一方で、解法Bもきちんとした合理的な幾何学的発想です。
AとBの大きな違いを考えてみましょう。
Aは「もともとあった平行関係を利用して、それを中心に展開している」ことです。
Bは「新たに平行な直線を自分で設定して、論理展開している」ことです。
図形の外に延長すると「交点S」という「一つだけ点が増えた」状況です。
対して、図形の中で補助線・平行な線を引くと「交点T,U」という「二つの交点が増えた」状況です。
交点が増えるのは、図形問題を解くためには負担が増える傾向があります。
その点も考慮して、「自分が考えやすい解法」をしっかり習得しましょう。
解法Bは少し「力技」的な面がありますが、「根気良く解決する能力」もまた「学力」です。
このように様々な三角形を考えることは非常に大事なことです。
そして、図形問題が一気に見えてくるでしょう。
男子小学生確かに、色々と考えると
一題で色々分かる気がする！
最も良いのは勉強の過程において、このような様々な考え方を身につけておくことです。
男子小学生色々な解き方が
あるんだね。
女子小学生色々な相似形を
考えると楽しい。
すると、試験本番で「Aの方が短い時間で解ける」と判断出来ます。
・回転した図形も、元の図形も「同じ図形」であることを強く認識
・「同じ辺の長さ」と「同じ角度」を図形に描きこむ
・たくさんの「同じ角度」から、相似形を見つけて相似比を考える
そして、「Aの解法を選択する」ことが出来るようになるでしょう。
「平行」などの基本的性質も、しっかり理解しましょう。
・直線が互いに交わらない
・直線が互いに「全く同じ向き」を向いている
・平行な直線同士の錯角は同じ
・錯角が同じ直線同士は平行
そのためには、「自分で図形や線を描いて」試行錯誤しましょう。
その「遠回りに見える道」が「学力を上げる最も近道」です。
様々な解法をきちんと理解して、身につけておくことが大事です。
次回は下記リンクです。
