前回は「歴史・地理の記述問題の記述式答案の書き方・例とポイント〜米国とドイツと日本の学校制度・簡単にまとめて比較・異なる点や特徴に気づく・模範解答例と自分の解答の比較〜」の話でした。
じっくりグラフを読み解く姿勢
単線型・複線型の学校制度に関して考えました。
単線型 = 進路が幅広い中から選べる
複線型 = 専門性が高く、選べる進路が限定される
問6に進み、日本国内、とりわけ関東地方一都六県の話です。
「都・県内の進学率」と「都・県外の進学率」の男女別の状況をまとめたグラフです。
社会のグラフにしては、かなり細かいグラフです。
こういう問題は、理科のように「じっくりグラフを読む」ようにしましょう。
男子小学生社会のグラフって、
難しそう・・・
社会でも理科でも算数でも、「グラフはグラフ」で同じです。
「社会だから」と考えずに、「グラフを理解すれば良いんだ」と考えましょう。
グラフを読み解く際に、最も大事なことは、「大まかな傾向をつかむこと」です。
男子小学生「大まかな傾向」って、
大きな特徴っていうこと？
そして、その「大まかな傾向」や「大きな特徴」の理由は何か？を考えましょう。
・「大まかな傾向」「大きな特徴」をつかむ
・「大まかな傾向」や「大きな特徴」の理由は何か？を考える
「大きな特徴」の理由と原因：「何が違うのか」を考える
一眼見て、左側の「東京以外」と右側の「東京」で大きく異なることが分かります。
男子小学生そう、「東京以外」と「東京」が
全然違うね・・
実際に都市・街の雰囲気も、東京と東京以外では大きく異なります。
この時、左右でグループ分けをして、「丸で囲む」などグラフに気づいたことを描くのも良いでしょう。
図と異なり、明確な数値のあるグラフは「大きな傾向」を読み取りましょう。
単に「大きく違う」よりも「何が違うのか」を考えるのが良いでしょう。
男子小学生何が違うのかな、
って考えるの？
あまり難しく考えずに、「グラフの大きな特徴」となる線を自分で引けると良いでしょう。
「グラフの問題」というと、理科の実験問題が多いです。
理科の実験問題では、直線や曲線のグラフがあって、その線から「傾向」を読み取ります。
男子小学生うん。
大きな傾向が大事だよね！
女子小学生グラフの線から、
傾向を読むのは出来るけど・・・
女子小学生自分で「線を引く」のは、
難しそう・・・
左右の大きく傾向が異なるグループの間には、明確な違いがあります。
そこに境界が見えてこないでしょうか。
男子小学生境界となる
線を引けばいいのかな・・・
少し「線を引く」ことを考えてみましょう。
グラフに線を描く：問題文のテーマとキーワード
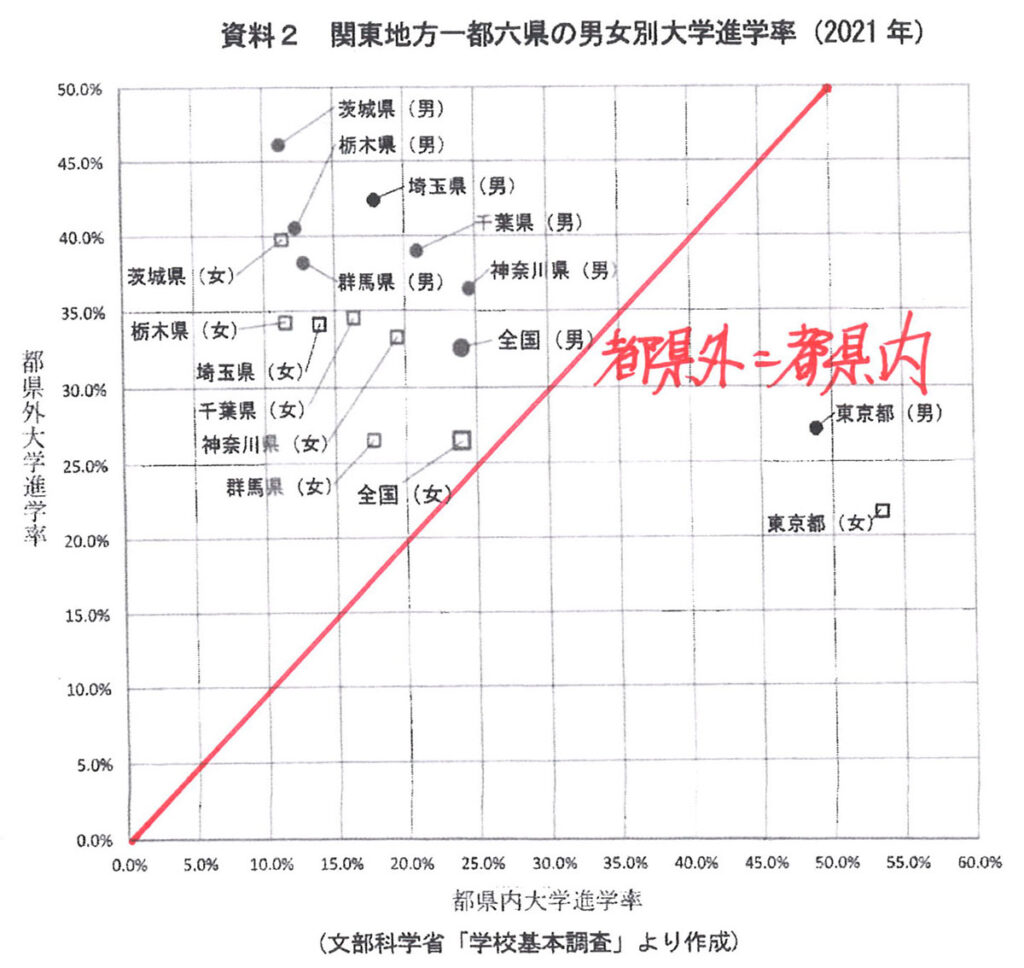
一本の「大きな特徴を示す」線を描いてみましょう。
「都・県内の進学率=都・県外の進学率」となる直線を描いてみましょう。
男子小学生この線は
分かりやすいね。
女子小学生大きな傾向が、
よく分かるね！
男子小学生この線は、
どうやって引くの？
「縦軸と横軸が比例=同じ」となる直線です。
そこで、同じとなる「20%同士」などの点と原点を結びましょう。
女子小学生この直線が
二つのグループの大きな境界になるね。
このように「大きな傾向を掴む」とグラフは良く分かります。
最近は、「情報」や「プログラミング」などの科目で「X軸とY軸」を勉強しているかもしれません。
すると、この直線は「X軸とY軸が同じ」あるいは「Y=X(X=Y)」ですね。
新たに引いた、この直線をもとに考えましょう。
直線の上は、なんでしょうか。
男子小学生「都・県外の進学率>都・県内の進学率」
だね。
女子小学生直線の下側は、
「都・県外の進学率<都・県内の進学率」だね。
女子小学生そして、直線の下側は、
男女ともに東京だね。
すると、一番大きな傾向は、
1.東京は男女ともに、都内の大学へ進学する割合が多い
2.他の６県は、県外への進学率が県内の進学率より高い
そして、「全国平均」のマークにも気をつけると、
3.他の６県は、全国平均よりも県外への進学率が県内の進学率より高い
です。
そして、この問題文のテーマになっている、「男女の違い」にも注目してみましょう。
女子小学生全部、男子より女子の
進学率が低い！
4.関東全ての地域で、男子より女子の進学率が低い
これらを、自分なりにまとめてみましょう。
A.関東全ての地域で、男子より女子の進学率が低い
B.東京は男女ともに、都内の大学へ進学する割合が多い
C.他の６県は、県外への進学率が県内の進学率より高い
D.他の６県は、全国平均よりも県外への進学率が県内の進学率より高い
男子小学生このA〜Dがポイントだってことは、
分かったよ・・・
男子小学生これって、全部書かないと、
満点にならないのかな・・・
採点基準は、採点者にしかわからないのが実情です。
「採点者にしかわからない」のですが、「書いた方が良いポイント」はあります。
女子小学生この場合は、
最も大事なポイントは何かな？
こういう時は、「問題文全体のテーマとキーワード」を考えましょう。
男子小学生「問題文全体のテーマ・キーワード」
かあ・・・
男子小学生「単線型」と
「複線型」！
女子小学生あとは、やっぱり、
「男女の違い」もある！
・「単線型」「複線型」
・男性と女性
「単線型」と「複線型」は、言葉自体はそれほど難しくありませんが、一般的に使う言葉ではありません。
むしろ、「この問題特有の考え方」です。
そして、「男性と女性」は誰でも分かることですが、この文章で非常に強調されています。
問6の答えは、上記の「A.関東全ての地域で、男子より女子の進学率が低い」は是非書いて欲しいです。
そして、「関東地方の男女別進学率」で「東京」と「東京以外」で大きく差があります。
こういう「項目で明確な差がある」場合は、それぞれの項目に対して特徴を書くと良いでしょう。
具体的には、「B.東京は男女ともに、都内の大学へ進学する割合が多い」です。
Bに対応する「C.他の６県は、県外への進学率が県内の進学率より高い」も「対比」として書きましょう。
「D.他の６県は、全国平均よりも県外への進学率が県内の進学率より高い」は「全国平均との対比」です。
これは「書いてあれば、なお良い」ですが、A〜Cで満点と考えます。
・文章のキーワード・テーマに沿った内容が最も重要
・読み取れる「対比的な特徴」を、対比するそれぞれの対象に対して書く
・2〜3つ程度のポイントを書く
男子小学生では、例えば、
A,B,Dを書いたら、どうなるの？
採点者次第ですが、「A,B,Cの方がベター」と考えますが、「A,B,D」に対しても「ほぼ満点」と考えます。
女子小学生自分でポイントを
まとめる練習してみよう！
次回は下記リンクです。
