前回は「図形問題・正六角形の考え方〜少しずつ面積を求める・分かっていることを図形に描く・並んだ点の長さの比を整理・対称性・対角線・連比と最小公倍数・相似形の面積比・問題4(2)解法A〜」の話でした。
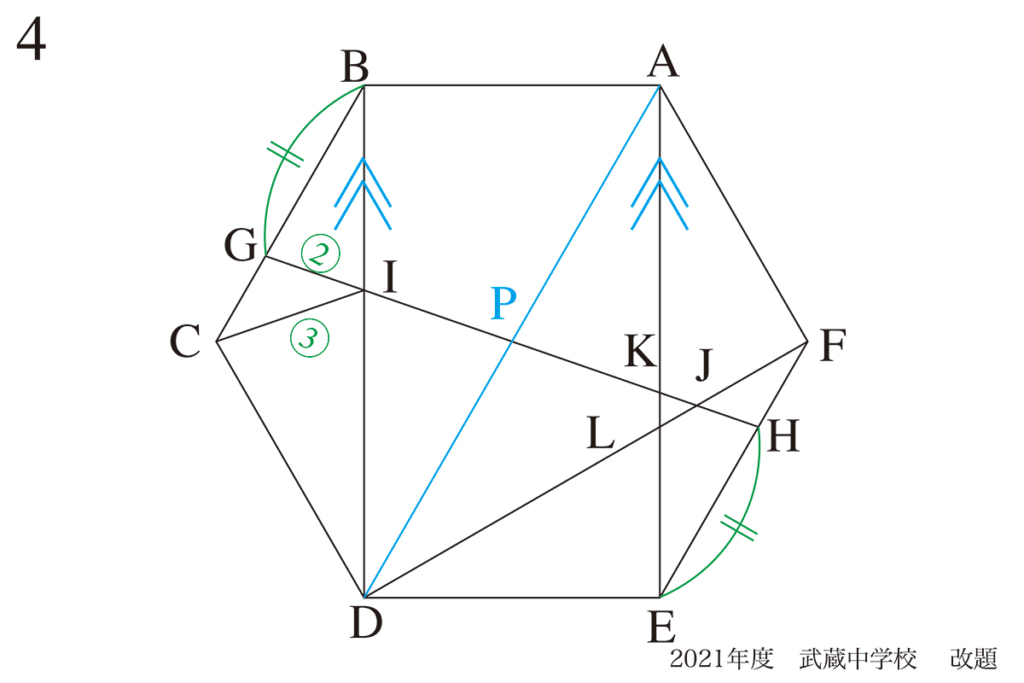
問題4(再掲載)

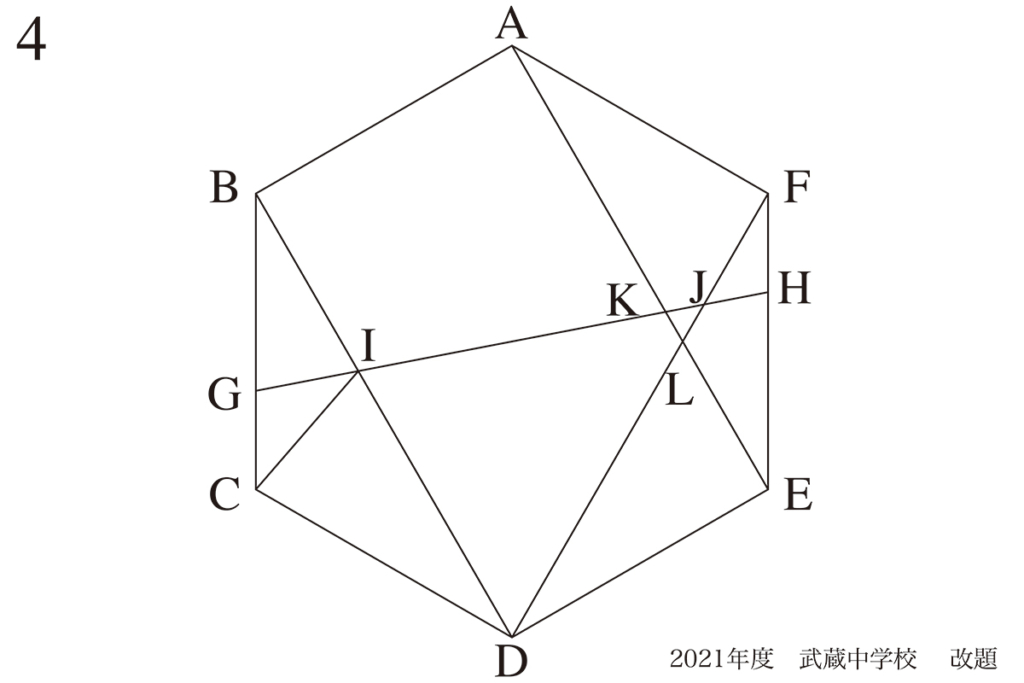
正六角形の大事な性質:対称性・平行
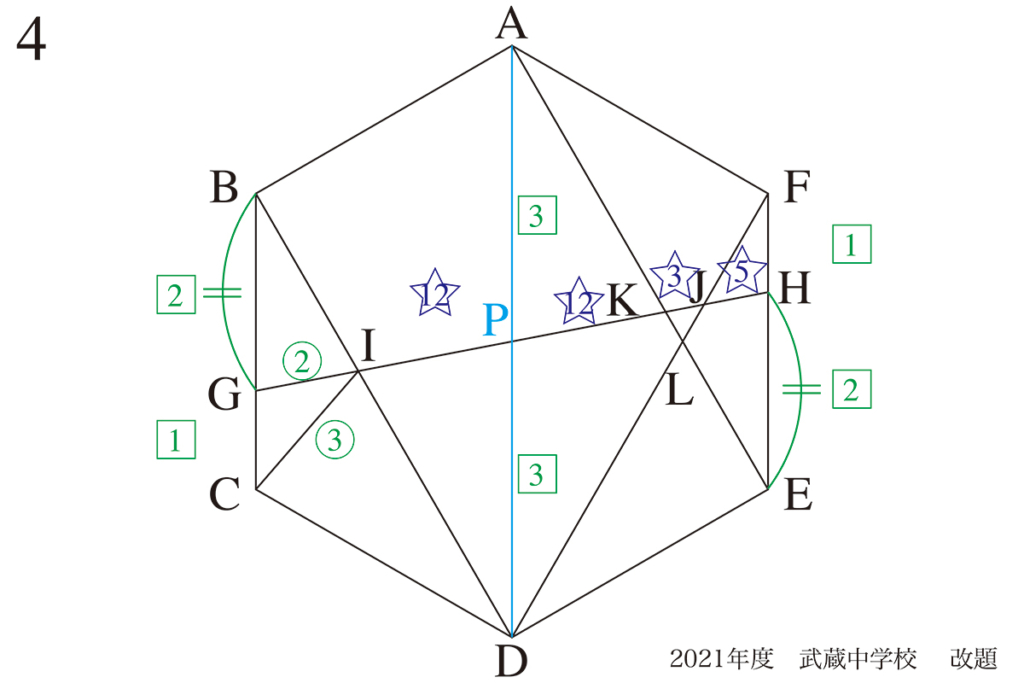
今回は、(2)を少し前回と少し異なる視点で考えてみましょう。
対称軸と中心を考え、△IJLの面積から△KLJを求めるところまで同一です。
この図形を見ていて、平行となる線を色々と探してみましょう。
平行な線の組み合わせはたくさんありますが、ちょっと気付きにくい組み合わせがあります。
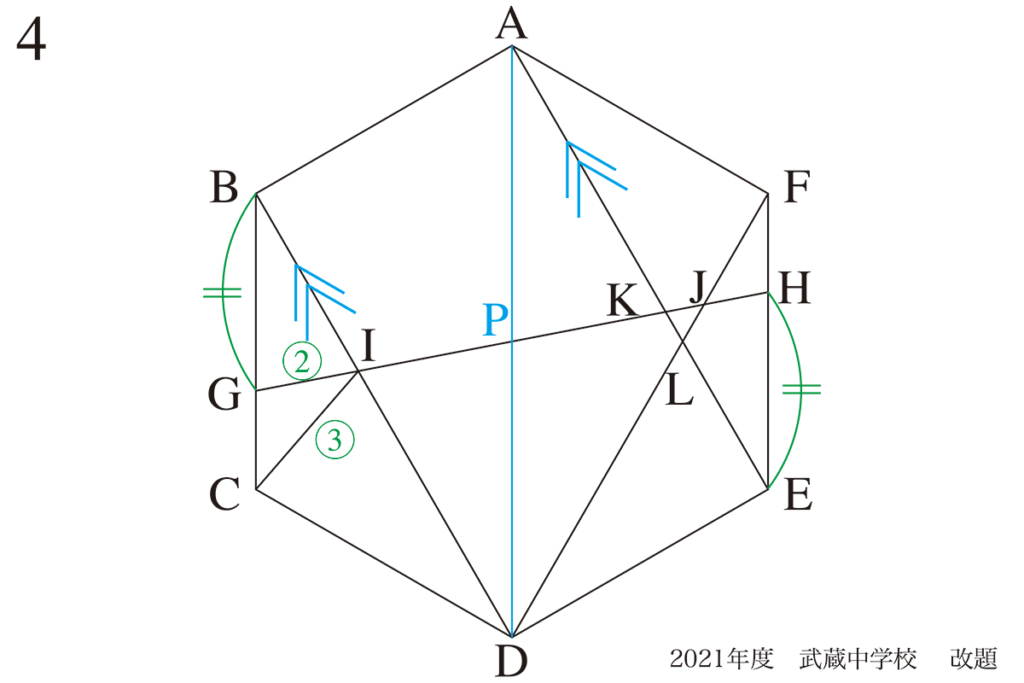
それは、「BDとAEが平行」です。
相似形の面積比:辺の比を2回かける
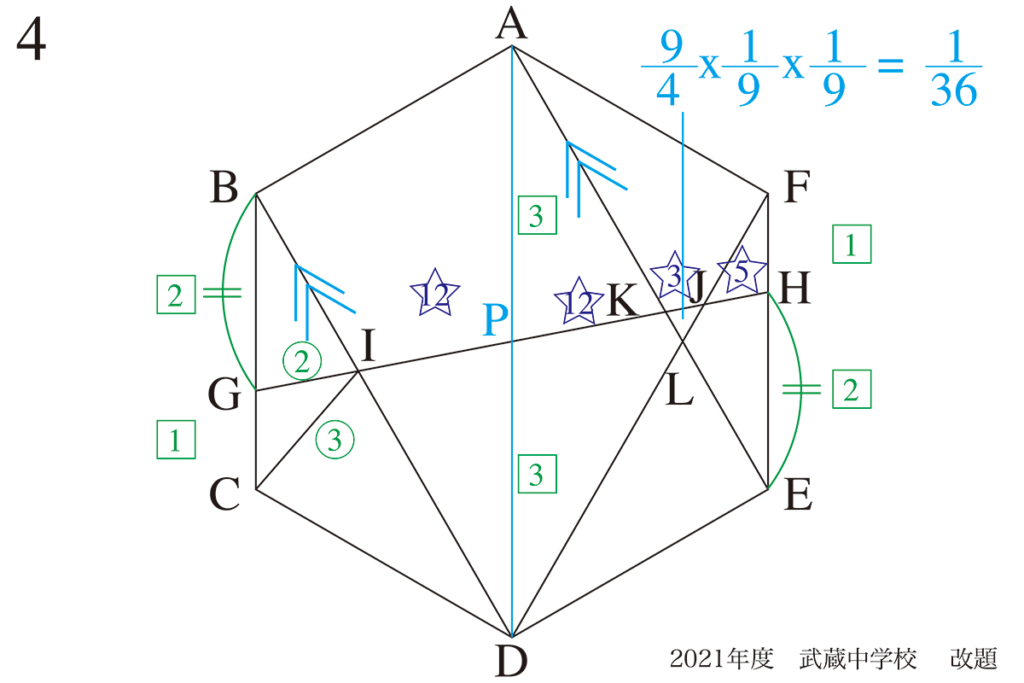
平行であることがわかれば、△KLJと△IDJが相似であることがすぐに分かります。
相似三角形の面積比は、辺の比を2回かける(2乗)と計算できます。
IP : PK : KJ : JHを求めて、JK : KI =1 : 9から、△KLJの面積が求まります。
「相似形の比=辺の比を2回かける(2乗)」は、しっかり理由を理解しておきましょう。
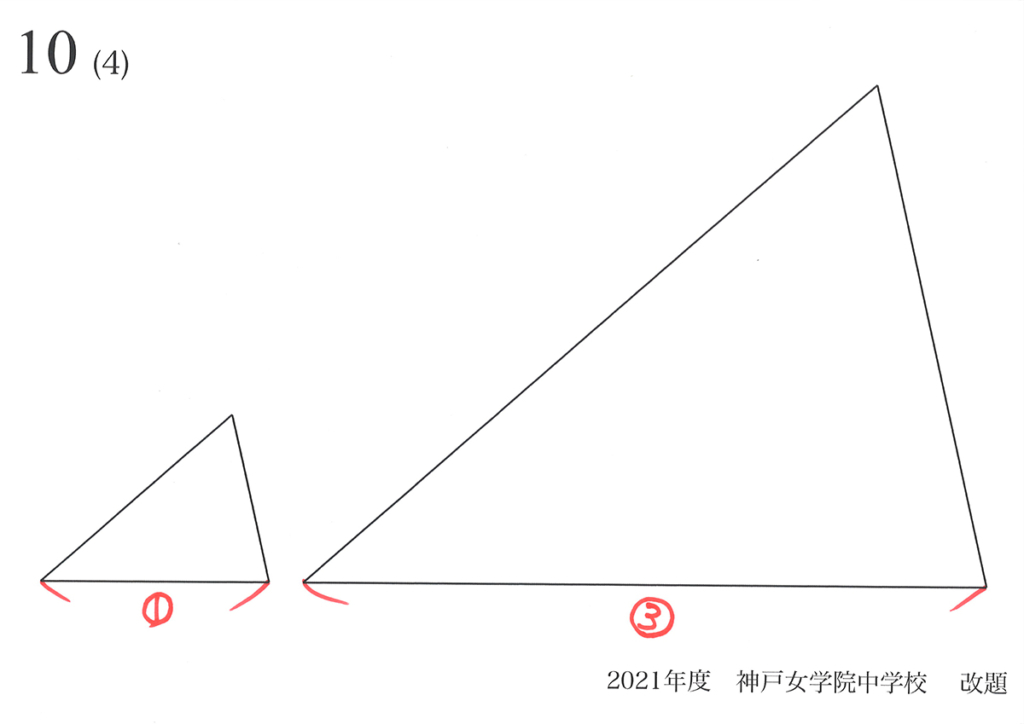
二つの図形が相似である時、
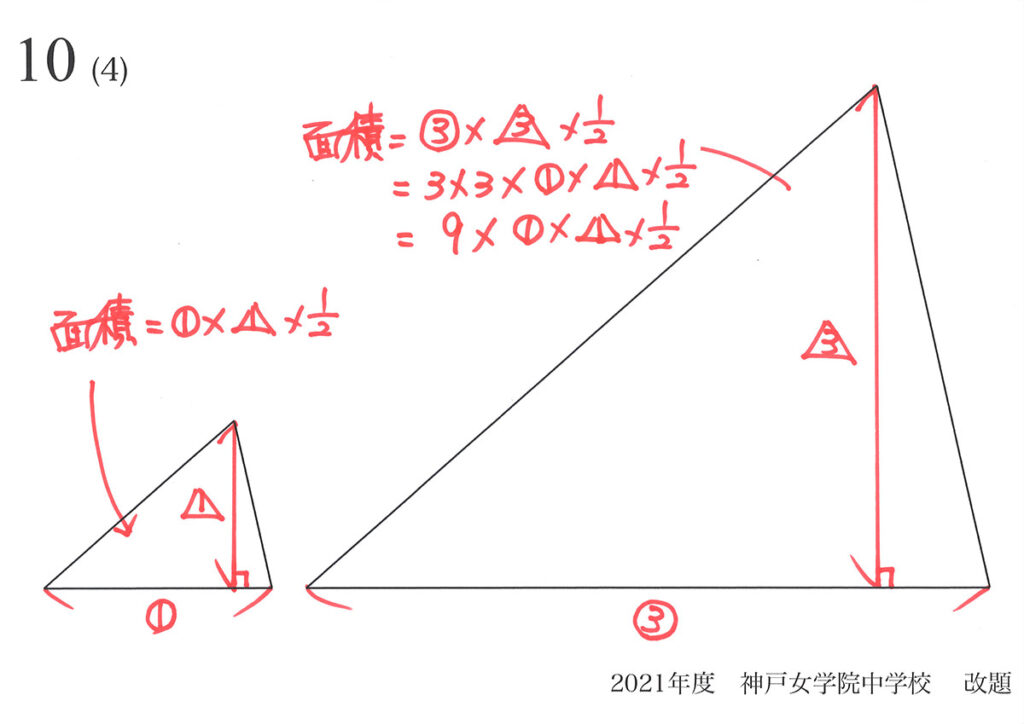
相似である意味を考えれば、面積比も理解できます。
面積比に関する話を、上記リンクでご紹介しています。
図形を異なる視点で見る:「自分の都合の良い角度」から見る
BDとAEが平行であることは、「言われてみれば当然」かもしれません。
 男子小学生
男子小学生言われたら分かるけど、
なかなか気づかないかも・・・
こういうことには、意外と気づかないこともあります。
この図形全体を、右回りにクルッと30°回転してみましょう。



あっ、
平行だ!
回転したら、一目で分かります。



確かにそうだけど、
不思議ね・・・
「BDとAEが平行」というよりも「四角形BDEAは長方形」という事実に気づきます。
これは、見れば一目瞭然です。
頭の中で回転させられれば良いですが、自分で「回転した図を描いてみる」のも良いでしょう。
試験場で試験用紙を回転させても良いでしょう。
図形問題は「自分の都合の良い角度」から見てみることも大事です。
「異なる視点から眺める」ことは非常に本質的で、大変効果的な考え方です。
「違う視点から考える」ことは様々な問題で、ぜひ考えてみましょう。
すると、算数(数学)のセンスが磨かれます。
この問題は、いくつかの視点が見えて色々な切り口が学べます。
これで円や正〜角形の図形問題は、解けるようになるでしょう。
次回は下記リンクです。



