前回は「実験問題攻略法 4〜熱の実験のコツと解き方・熱が広がってゆく具体的イメージ・理科実験の体験を思い出す・熱が伝わり広がる速さ・速さを矢印で表現・見方を変える・現象の共通点を探る姿勢〜」の話でした。
熱の実験のコツと解き方：まず最初と最後を比較
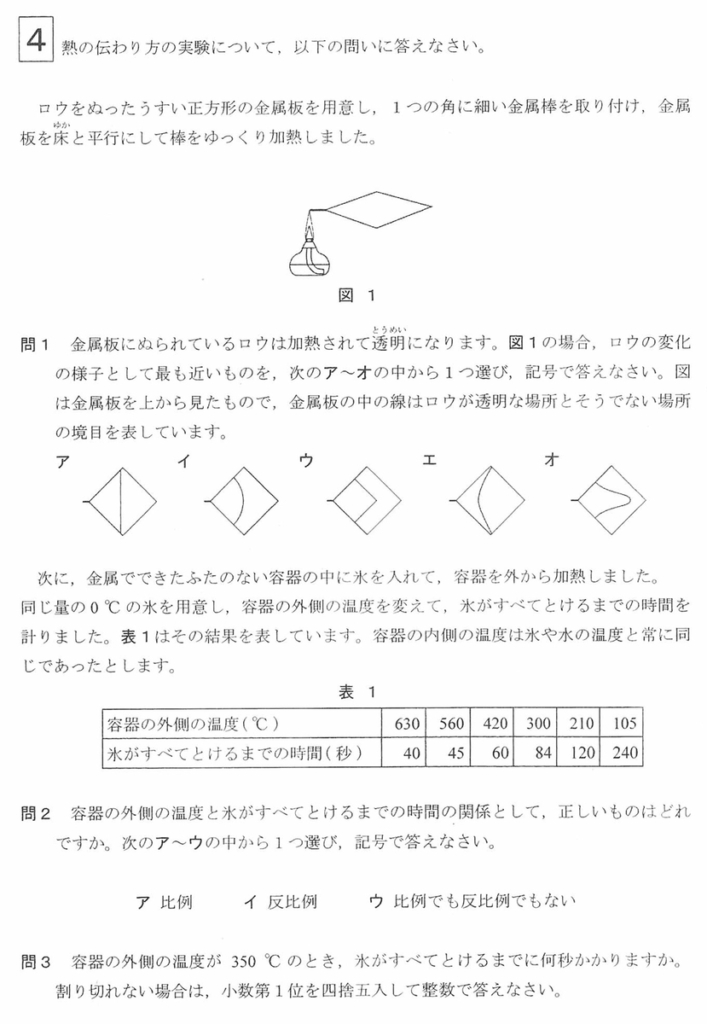
開成中学校の2019年理科の問題4を考えてみましょう。
問1が終わり、今回は問2,3を考えてみましょう。
問2では、温度と時間の関係が「比例、反比例、どちらでもない」のどれかです。
こういう時は、まず最初と最後をみて、比較しましょう。
・まず最初と最後を比較：時間が経過しているので、「大きな変化」があるはず
・最初と中央付近、中央付近と最後を比較：変化の仕方の違いを比較すると何か分かる
パッとみて「温度が1/6になっていて、時間が6倍」になっています。
これで、
男子小学生よしっ！
反比例だ！
「反比例」と気づく人が多いでしょう。
表やグラフが出てきたら、順に追ってゆくよりも、最初と最後を見て全体の様子をつかみましょう。
比例と反比例の本質：「掛け算したら同じ」ではなく「反対に比例」
比例に関しては分かりやすいのですが、反比例に関して、分かりにくい面があるかもしれません。
男子小学生「反比例=掛け算したら同じ」
だよね！
「反比例=掛け算したら同じ」と、覚えている方がいらっしゃるかもしれません。
男子小学生そうだけど、
違うの？
それでも良いですが、基本的に反比例は文字通り「反対に比例」です。
ですから「片方がA倍になったら、もう一方は1/A倍」という考え方にしましょう。
片方がA倍になったら、もう一方は1/A倍
上記の表で、
男子小学生反比例=掛け算したら
同じかな？
「6つの温度と時間を掛け算」してチェックしても良いでしょう。
その考え方は時間もかかり本質的ではないので、イメージが沸きにくいです。
105が「630の1/6」であることは、暗算でもできそうです。
これでイが答えですが、念の為もう一つ確認しましょう。
これも分かりやすい数字を選びます。
温度は、「210がちょうど630の1/3」です。
対して、時間を確認すると「ちょうど3倍」です。
本来ならば「全部確認するのが良い」ですが、試験は時間も大事です。
ここまでチェックしたら自信持って、
男子小学生よし、反比例だから
答えはイ！
こう考えて、次の問題に進みましょう。
イ
実験の誤差：簡単な数字を選んで計算
女子小学生ひょっとしたら、他の数字が
反比例でなかったら、どうするの？
男子小学生反比例と思ったら、
チェックしないところが違ったら？
このように疑問に思う人が、いらっしゃるかもしれません。
筆者は「そういう出題はない」と考えます。
学校で実験をして、重さを測ったり、温度を測ったりした経験があると思います。
実験は、上記の表のように「ビシッと綺麗な数字」には、まずならないです。
本来は、必ず誤差があります。
なんらかの現象は、算数のように「ピッタリ行く」ことは非常に少ないことです。
測定する機器に、誤差がある可能性もあります。
男子小学生確かに、実験の時に
「思っていた数字とちょっと違う」ことってあるね・・・
仮に上記2つ以外が、完全に反比例ではなく「少しずれていてもOK」です。
また、上記2つ以外が「反比例ではなく」大きくずれている「ひっかけ問題」はないでしょう。
女子小学生それじゃ、二つくらいで
確認すれば良いね！
実験の数字は、大まかな傾向が大事なので、ご安心下さい。
問3へ進みます。
反比例は、本質的には「片方の数字がA倍なら、もう一方が1/A倍」です。
350℃が出てきましたので、「350と組み合わせて計算しやすい数字」を探すのが良いでしょう。
この場合、70を公約数とする210が良いです。
「350/210=5/3」と暗算でも出来るので、210℃の時の120秒の3/5が答えとなります。
「掛け算して一定」で考えますと、例えば、630×40/350を計算することになります。
これは「630と350の公約数が、70」ですから簡単です。
場合によっては時間もかかり、計算ミスの可能性も高まります。
反比例などの計算は「基本に忠実に、そして簡単な数字を選んで」行いましょう。
72秒
次回は下記リンクです。
