前回は「実験問題攻略法 3〜水溶液の実験のポイント・解き方・グラフを理解する大事さ・グラフの傾きに注目・大きな方向性を把握・急激な変化と自然な変化・自然現象をイメージ〜」の話でした。
熱が広がってゆくイメージ：理科実験の体験
開成中学校2019年理科の問題4を考えてみましょう。
「暗記しなければならないこと」も多い面もある理科。
実験の問題は「思考力を問うのに最も良い」ので、様々な学校で出題があると思います。
今回は問1を考えてみましょう。
まず、金属板の端を熱しています。
問1では、金属板に塗ったロウが、加熱されて透明になるのが、どのように広がってゆくか、です。
女子小学生熱が広がってゆくのは、
分かりにくいけど・・・
「加熱したら、熱が広がってゆく」のは自然現象です。
太陽の熱で熱せられる、など様々なことがあります。
こういう「自然現象」は「偏らずに」「なめらかに」広がってゆきます。
女子小学生確かに、なんでも自然現象は
「自然な感じ」だよね・・・
・加熱・溶解などの現象を、具体的にイメージする
・理科実験の体験を思い出す
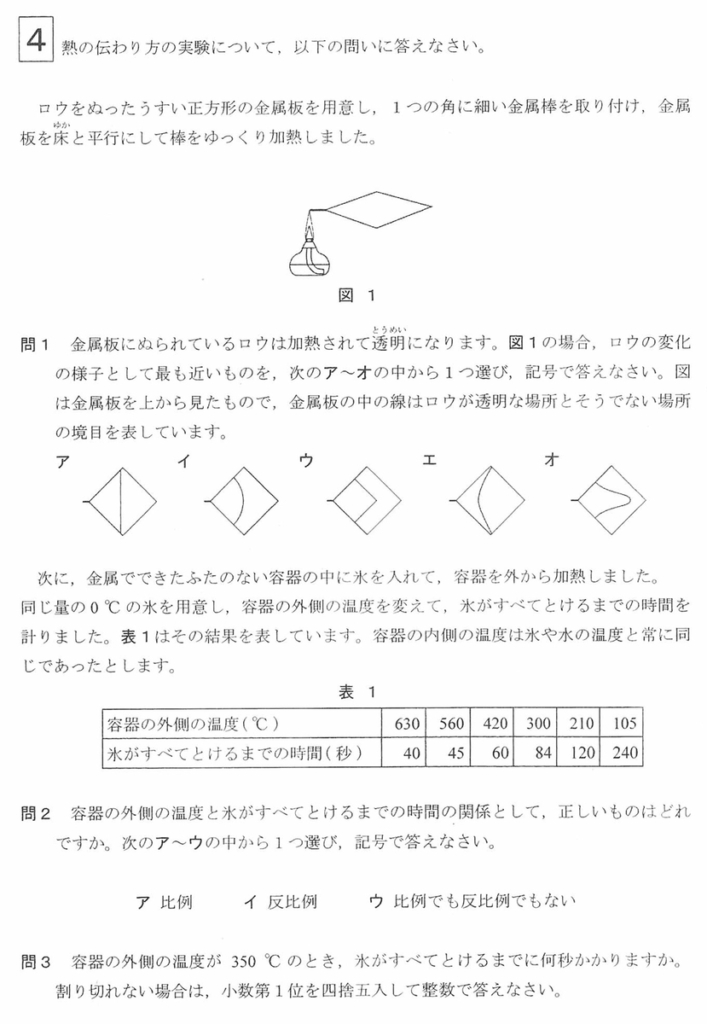
「均等に広がってゆく」イメージを、金属板に描いてみましょう。
図1に広がってゆく感じを描いてみました。
ここでイと分かります。
イ
熱が伝わり広がる速さ：速さを矢印で表現
もう少し考えてみましょう。
上記の通り、「ロウが溶ける＝熱が伝わる」と考えると、何か考えられますか。
男子小学生何か・・・
って何だろう？
女子小学生熱が伝わるのは、
熱が広がって、移動していくから・・・
男子小学生熱の移動も
速さがありそうだね。
「溶ける範囲が広がる速さ＝熱の伝わる速さ」とも考えられます。
「熱の伝わる速さ」を矢印で考えてみましょう。
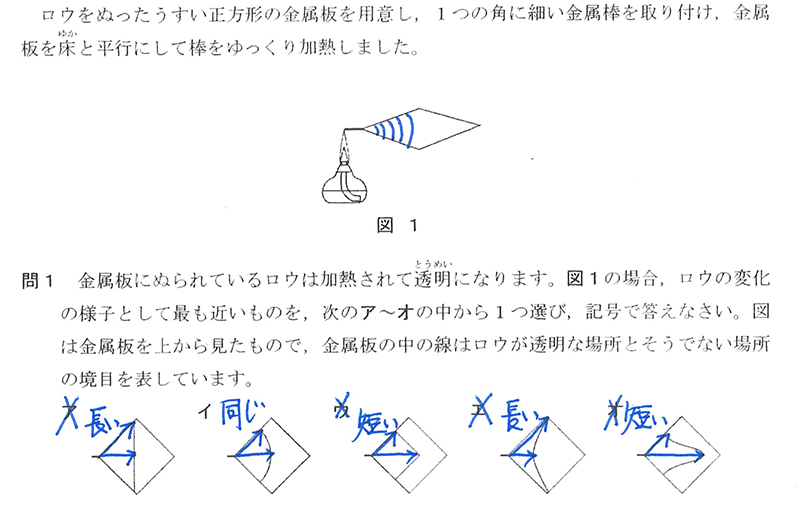
アとエ：斜め方向だけ長くて、熱の伝わりが速い
ウとオ：斜め方向が水平方向よりも短くて、熱の伝わりが遅い
イ：円形になっていて各方向の熱の伝わる速さが同じ
これらの理由からも、答えはイとなります。
アと迷う方が、いらっしゃるかもしれません。
下記のように考えてみましょう。
この問題では金属板の端を熱しました。
例えば、「金属板の真ん中を熱する」ことを考えてみましょう。
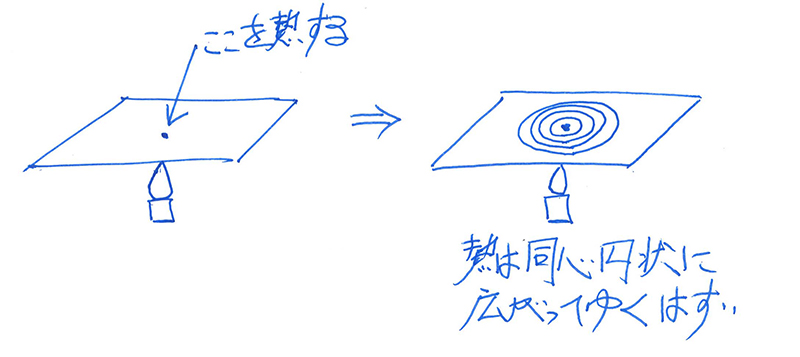
真ん中を熱すると、熱が同心円状に広がってゆくはずです。
女子小学生この広がってゆく感じは、
分かるね！
学校でやった実験や、目玉焼きを焼くイメージを考えてみてください。
自然現象では、広がってゆくのは基本的に円形です。
長方形に広がったり、歪な形で広がることは、特殊な条件でない限りありません。
波紋も同様です。
水にポチャンと石を投げることを考えると、波紋が円形上に広がってゆきます。
見方を変える：現象の共通点を探る姿勢
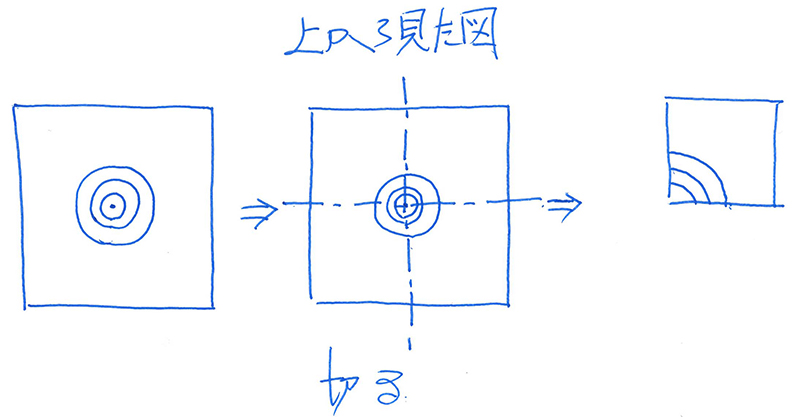
このイメージのように、「端を熱する」などを別の視点で考えてみるのも良いでしょう。
例えば、「金属板の熱する位置を中心に切ってみる」イメージを考えてみましょう。
円形に広がってゆく=「右上だけ＝左下の端を熱する」と考えると、
女子小学生角から円弧で
広がってゆくね！
1/4円になって広がってゆくのが分かります。
こういう問題はイメージして、すぐに
男子小学生あ、
これだ！
分かれば良いです。
悩んでしまう時は、
男子小学生端ではなく、
中央だったら・・・
男子小学生一体、
どうなるだろう・・・
自分で「少し条件を変えて、考えてみる」のも良いでしょう。
・少し状況を変えて考えてみる
・状況が少し変わっても、起こる現象には共通点がある
そのように考えると応用範囲が広がってゆきます。
算数や理科の問題は、
男子小学生・・・・・
問題文をじ〜っと眺めていても、なかなか分からない場合があります。
そういう時は問題文の中の絵、あるいは自分で余白に絵を書いてみて、
男子小学生こうかな？
こういうことかな？
「描きながら考えてみる」のが良いでしょう。
「イメージすること」は正しい答えに結びつき、得点がアップするでしょう。
次回は下記リンクです。
