前回は「図形の面積のコツ・ポイント〜「どの辺の比を求めるか」を明確に・上手い相似形が見つからない時・特徴的な方向を最重視・問題10(3)解法B〜」の話でした。
問題10(再掲載)

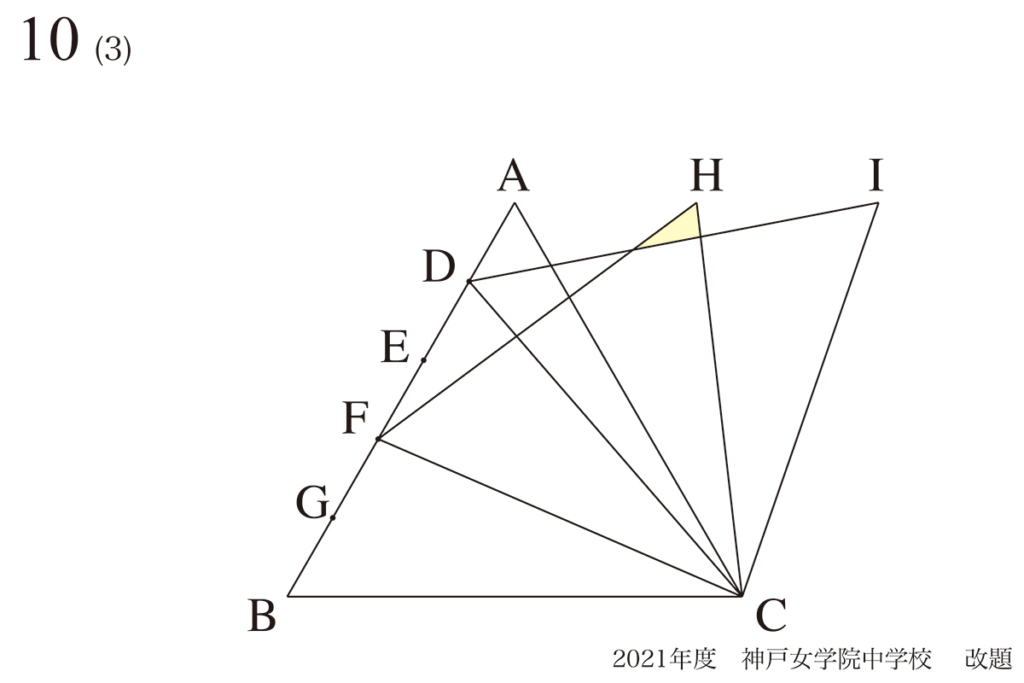
5点並んだ辺の比:連比を考える
(2)を利用して、黄色い部分の面積を求めましょう。
(2)の面積を利用して黄色い部分の面積を求めるには、HJ :JC=2 :21とNJ : JIが分かれば良いです。
・「問題を解くには、Aが分かれば良い」という「Aを考える」姿勢
・「Aを知るためには、どのようなことが分かればよいか」を考える
・少しずつ、着実に答えに近づいてゆく姿勢
そこで、「なんとかNJ : JIを求めよう」と考えます。
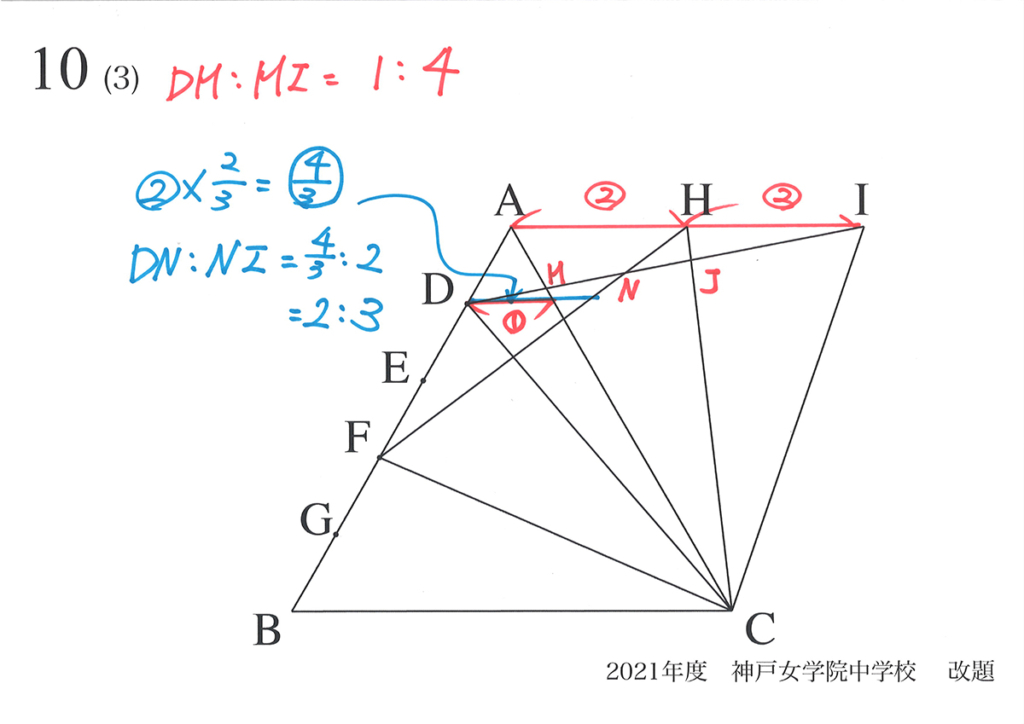
前回は、DN :NIまで求めました。
下図において、一直線状に並んだD,M,N,J,Iがあります。
この直線上のDM : MN : NJ : JIを求めて、NJ : JIを求めてみましょう。
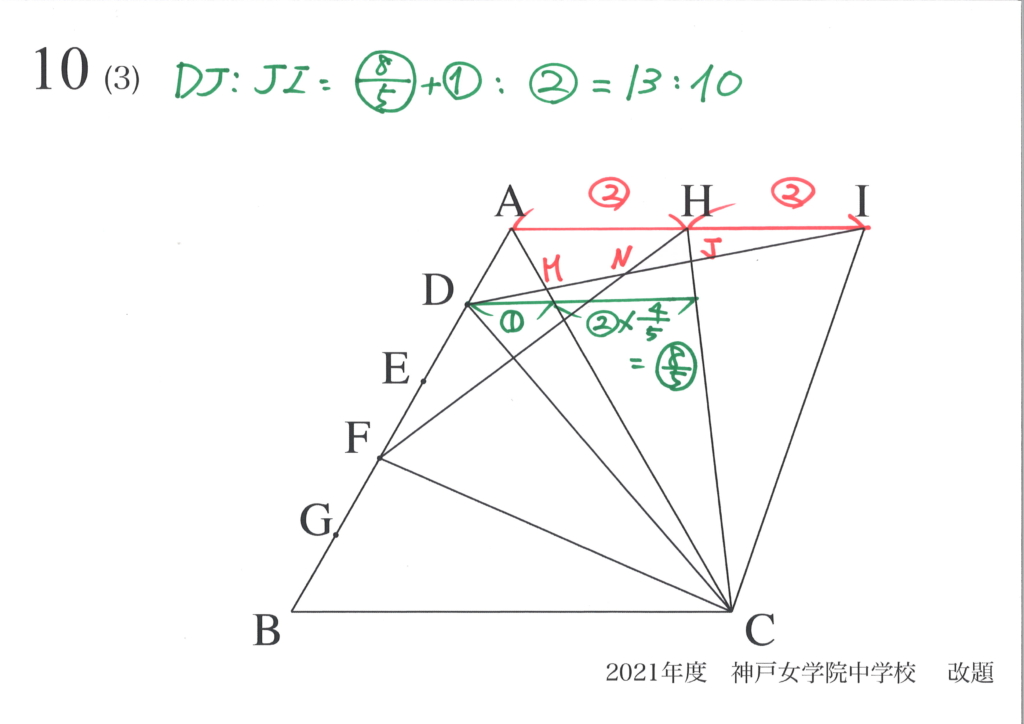
緑色の直線の長さは、二つに分割して求められDJ :JIが求まります。
DJ :JI = 13 : 10となり、だいぶ辺同士の比が分かってきました。
たくさん名前をつけると混乱するので、このように計算過程の点は図示して、比を考えて行きましょう。
これで、DM : MN : NJ : JIに関わる辺の比がわかりました。
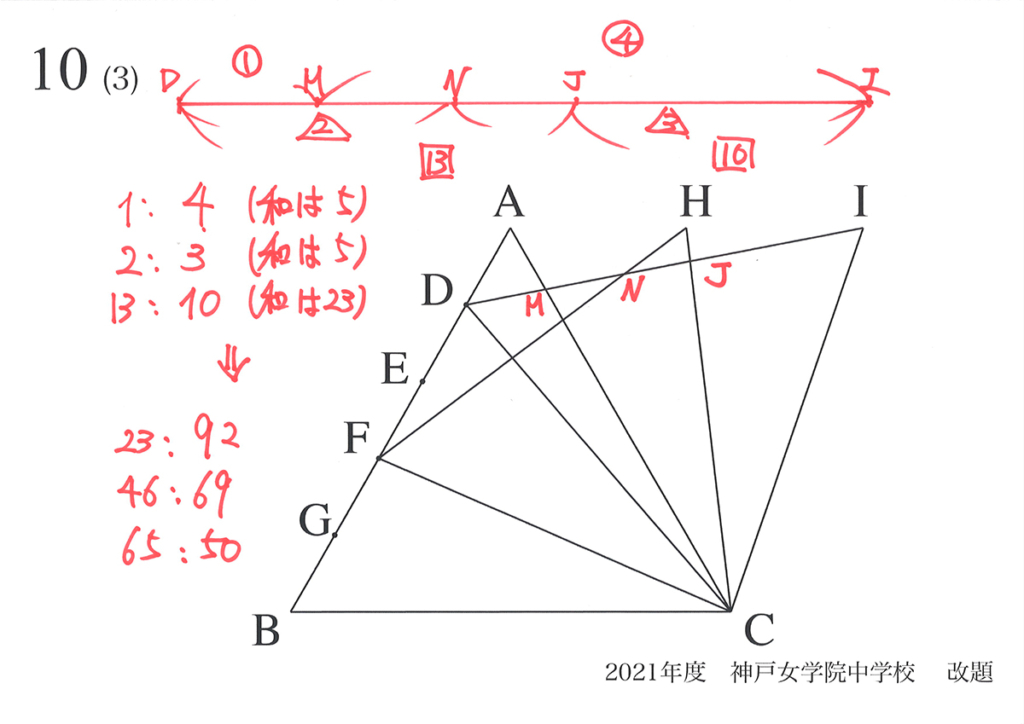
それぞれの比の和が5,5,23なので、「最小公倍数の5×23=115」を使って、比を按分しましょう。
DM : MI=1 :4→(23をかけて)→DM : MI=23 :92
そこで、全体DIの長さが23+92=115になるように、比を按分して、各辺の長さを求めます。
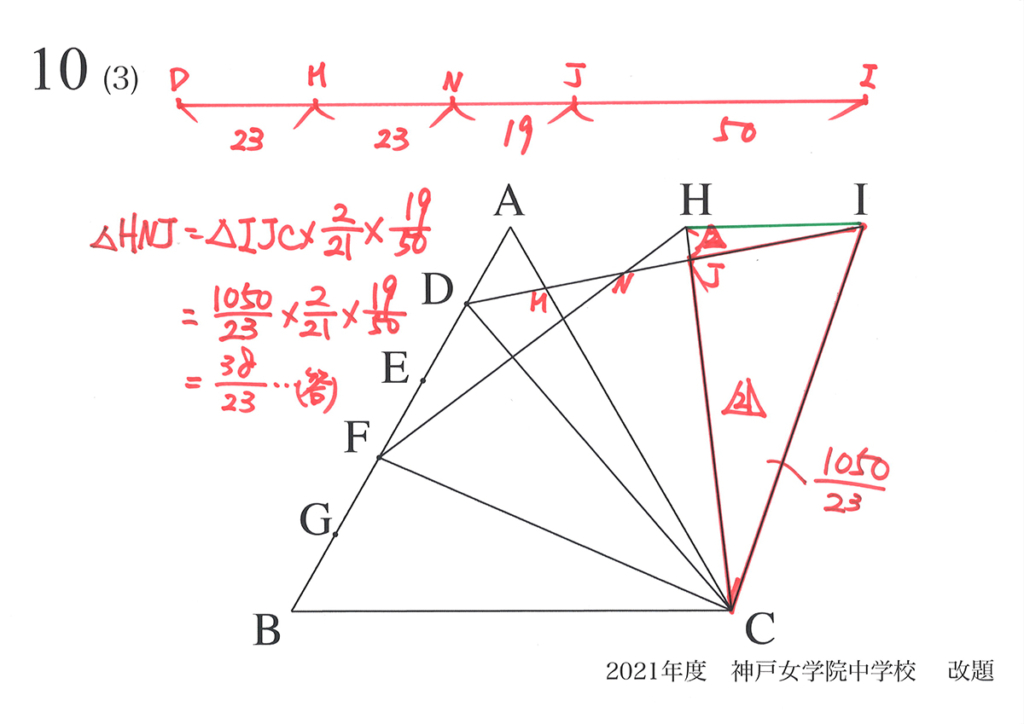
上の図の通り、比が求まりました。
NJ : JI=19 : 50ですから、ここからは面積が求められます。
(1)を利用したときと、答えが一緒になりました。
根気よく考える姿勢:「何かを成し遂げる」に最も大事な力の一つ
ちょっと長い時間がかかり、(1)を利用した方が早くできます。
 男子小学生
男子小学生これは、(2)の解き方が
良くないのかな・・・



これは、ちょっと
大変すぎるかも・・・
「時間がかかる」意味では(2)の解法は、試験では避けた方が良いでしょう。
こういうことも「実際にやってみたらわかる」ようになります。
そして、



これは、
こういう方向でやったらいいかな・・・
「図形問題に対する勘」が少しずつ磨かれます。
少し遠回りですが、こういう計算力は非常に大事です。
入試で「単なる計算問題」や「穴埋め式の計算問題」がよく出されます。
「単なる計算問題」よりも、「計算力を見る問題」は良い問題です。
「少し時間がかかっても、やり遂げる力を試す」姿勢です。
あるいは「地道な計算力が求められる」問題によって「計算力は測られるべき」と考えます。
・問題を解く途中で諦めずに、しっかり進めてゆく大事な力
・「こう考えれば解けるはず」という、目標を明確に持つ大事さ
・根気や努力は「将来何かを成し遂げる」ために最も大事な力の一つ
今回、4つの連続する辺の比を求めるという、少し根気のいる解法を実践してみました。
特に最難関校志望の方は、ぜひ根気を磨いてみましょう。
「少し遠回りで時間がかかる」でも「手が止まってしまう」よりは良いことがあります。
根気を磨くことは、学力の大幅な増強になるでしょう。
次回は下記リンクです。


