前回は「複雑な図形問題のおすすめな考え方〜正三角形・相似形を見つける・平行な線に注目・相似形が見つからなければ自分で「相似形をつくる」・問題を解く勘を磨く・「遠回り」や「無駄」から分かること・問題10(2)解法〜」の話でした。
問題 10（再掲載）
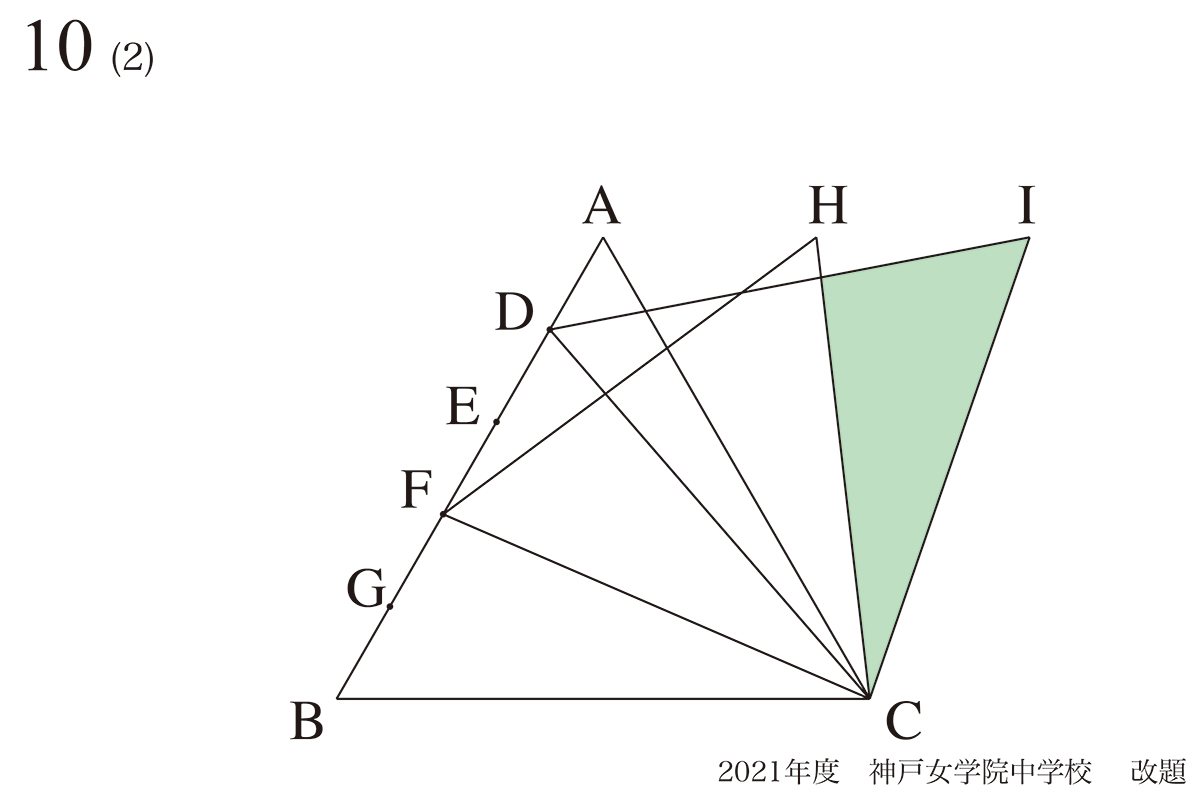
図形的センスと補助線のコツ：求めたい比と平行から相似形を探す・つくる
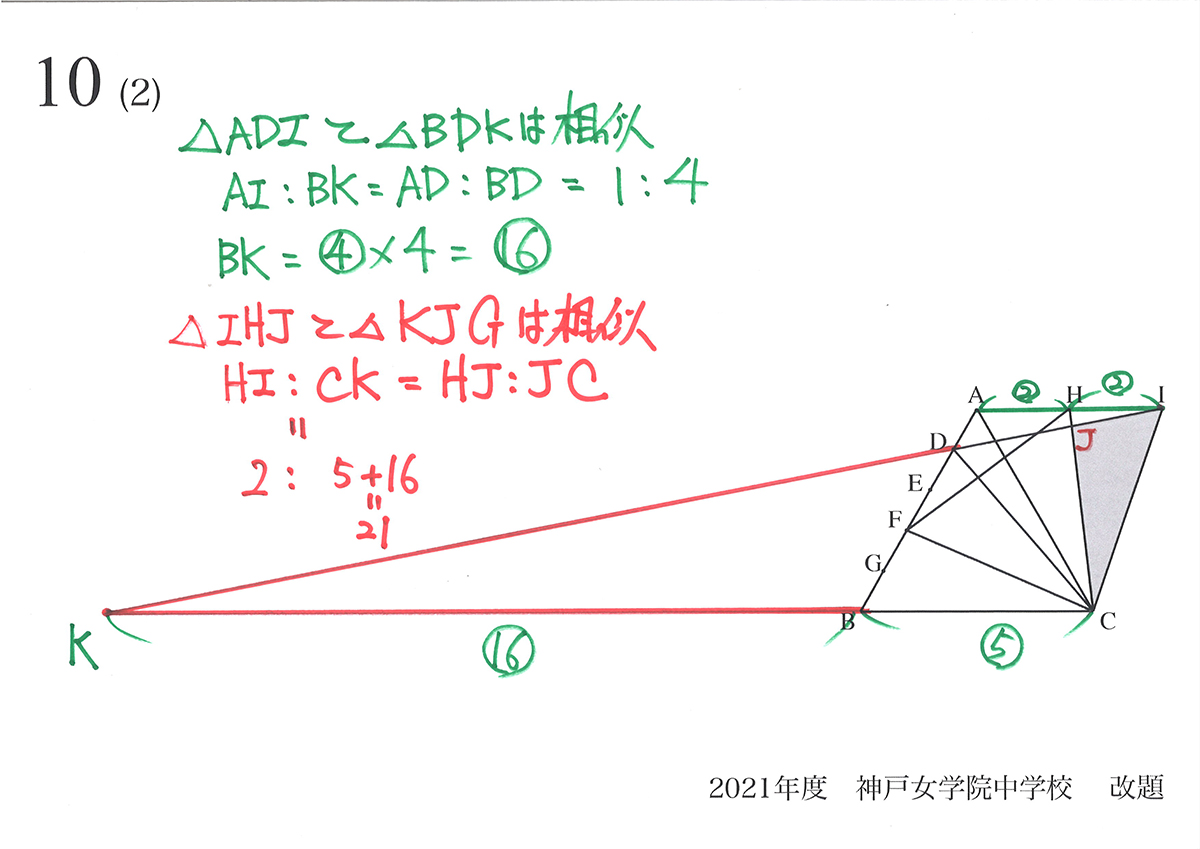
・「相似形が必ずある」と考えて、相似形を探す
・相似形が見つからないときは、「相似形を作って考える」姿勢
この問題では「AIとBCが平行」であることが、最も大事な性質です。
そして、平行な線がある場合は「相似形を探す・つくる」ことを考えます。
・「問題を解くには、Aが分かれば良い」という「Aを考える」姿勢
・「Aを知るためには、どのようなことが分かればよいか」を考える
・少しずつ、着実に答えに近づいてゆく姿勢
(2)の面積を求めるために「HJ : JCを知りたい」と考えて、図形の外に出て補助線を引きました。
かなり大きく「図形の外」に出ましたが、「知りたい比=HJ : JC」は分かりました。
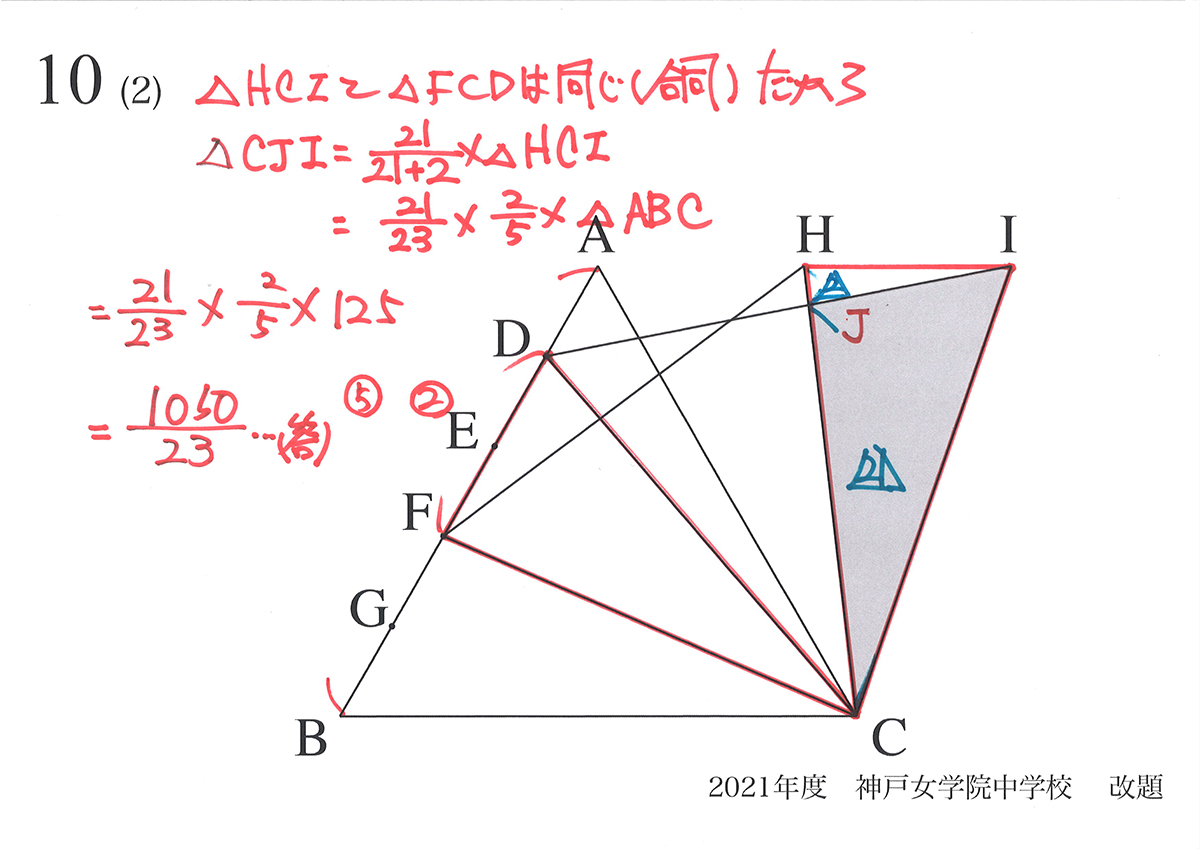
では、最終的に面積を計算すると、上のようになります。
答えは、1050/23です。
正三角形IDCの大きさの大体の予想：図形の勘を磨く
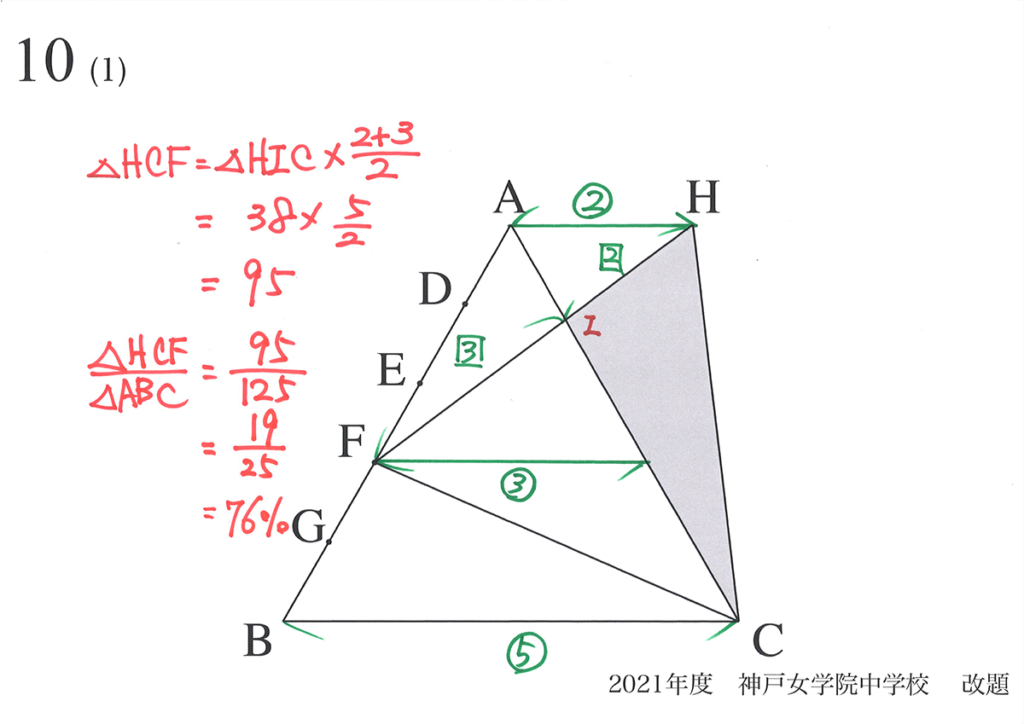
(1)で問題文にない寄り道をしました。
正三角形HFCの面積が、元の正三角形ABCの面積と比較して「どのくらいの大きさか」を考えました。
同じように、正三角形IDCの面積を求めて「正三角形ABCと比較」してみましょう。
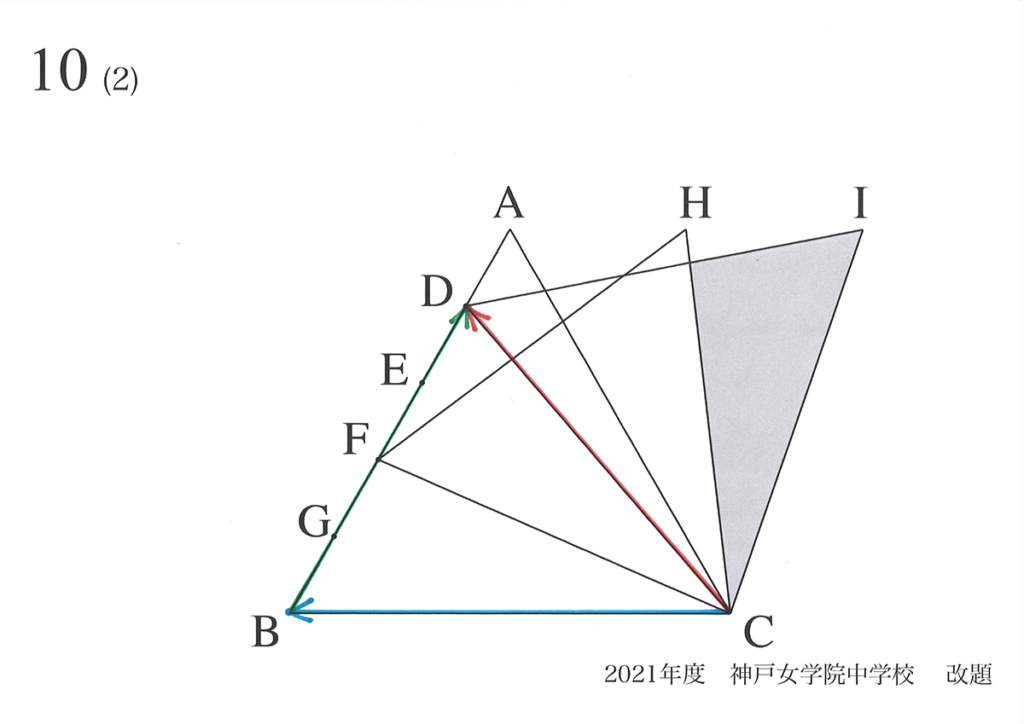
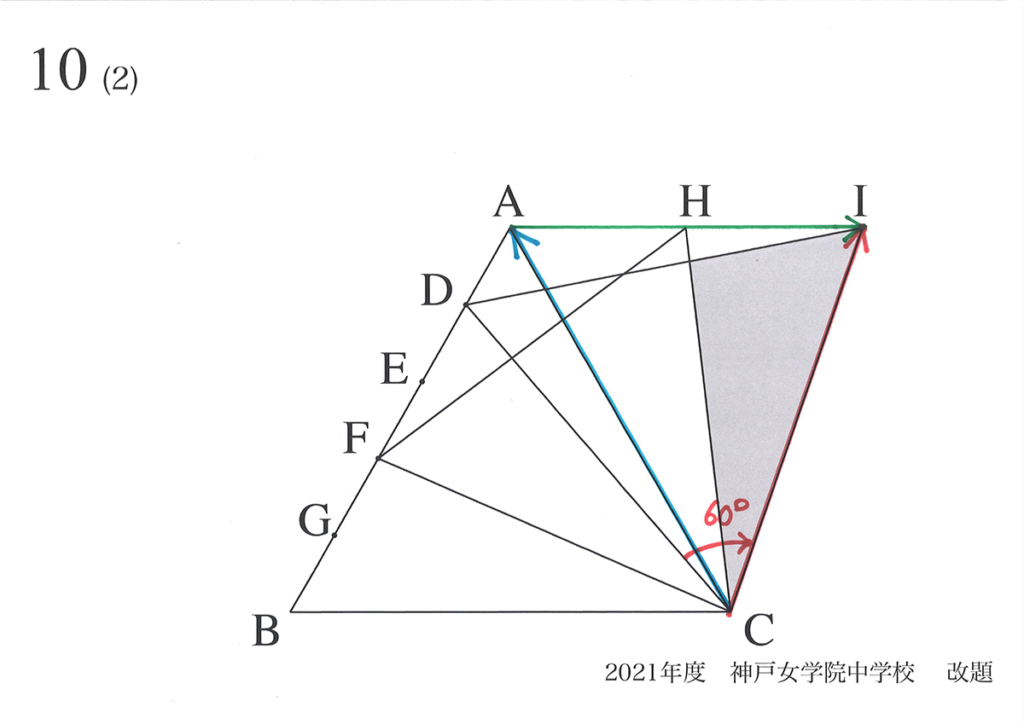
「矢印の考え」で辺AB上に点を取った時に、次々と連続的に正三角形が作られるイメージが出来ました。
男子小学生正三角形IDCの大きさって、
正三角形HFCの大きさに似ているね・・・
女子小学生ほとんど
同じ大きさにも見えるけど・・・
女子小学生ちょっと
違いそうな気がする・・・
男子小学生正三角形IDCと正三角形HFCって、
同じ正三角形だから、相似だね。
二つの正三角形HFCと正三角形IDCが相似形で、「相似系の面積は相似比に応じて変化する」事実があります。
男子小学生だから、面積は
辺の長さの比と一緒に大きくなるね。
女子小学生そうね。
だから、HFとIDの長さを比較すればいいのかな？
男子小学生DCとFCの長さを比較しても
良さそうだね・・・
計算する前に、予想してみましょう。
「正三角形HFCと正三角形IDCは、どちらが大きいか」を、少し考えてみましょう。
ちょっと考えてみて、予想した上で計算してみましょう。
次回は下記リンクです。
