前回は「おすすめの図形問題の解き方・考え方〜図形を矢印で考える・図形の回転=矢印の回転・矢印から分かる大事な図形の性質・問題10(1)〜」の話でした。
問題 10（再掲載）
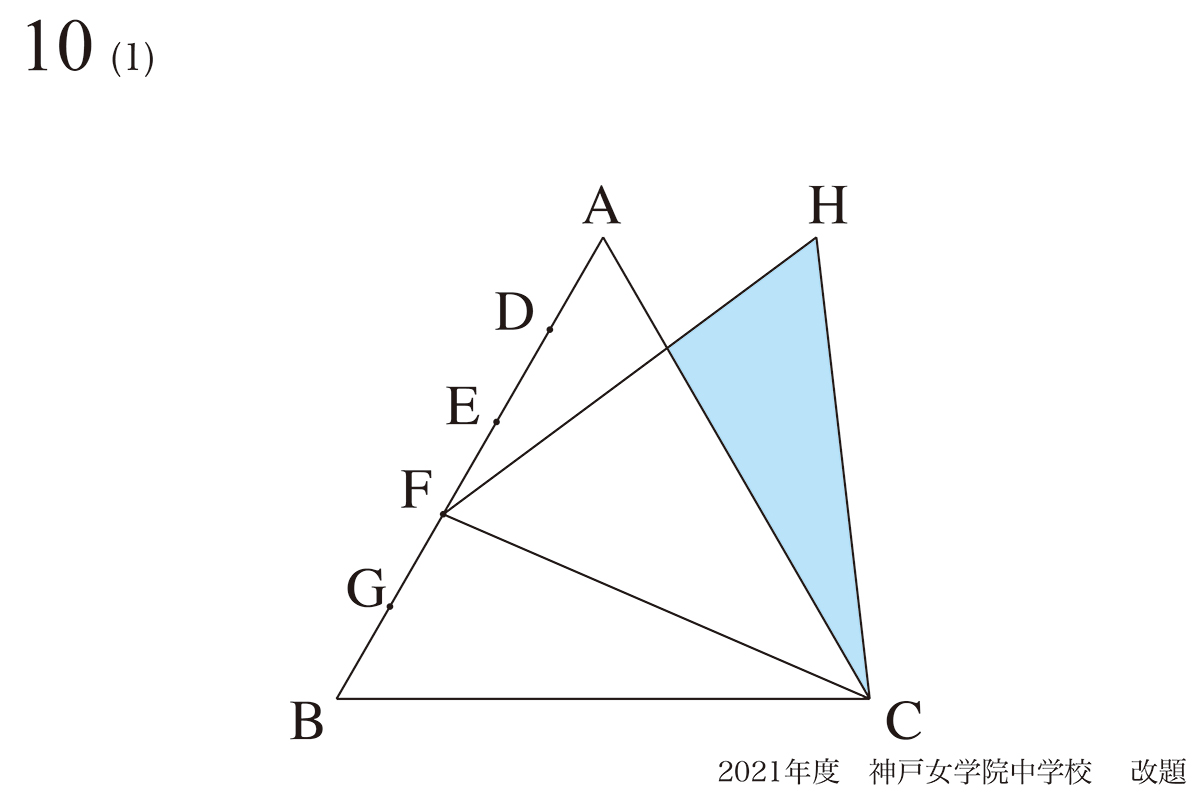
図形の性質：平行と相似形
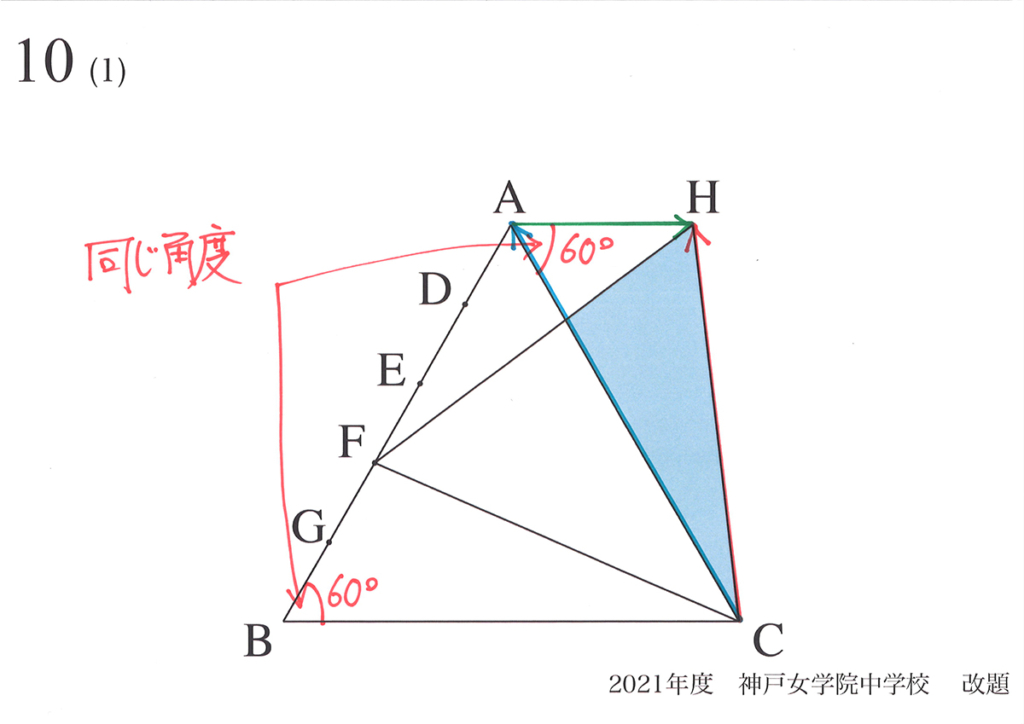
この問題を解く鍵は「AHとBCが平行」と「BF=AH」です。
今回は面積を求める問題ですが、図形問題では、まず「図形の性質」を考えるようにしましょう。
・求めるものが「面積・長さ・角度」など何でも、まずは「図形の性質」を考える
・点と点を結んで、矢印を考えて「図形の位置関係」を考える
・分かった図形の大事な性質を図形に描きこんで考える
「解く鍵」が見つかったので、解法へ行きます。
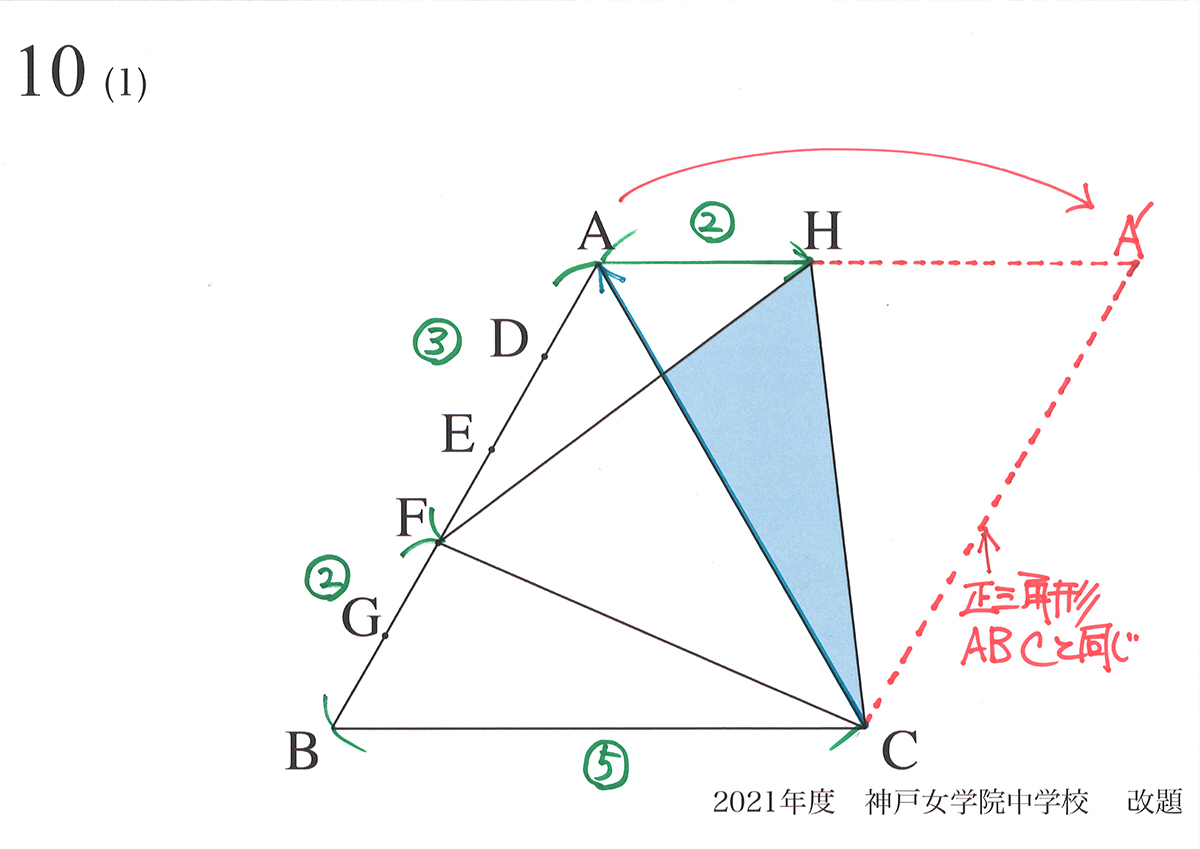
「辺を五等分」しているので、「辺BCの長さ=辺BAの長さ=辺ACの長さ=5」と置きましょう。
ここで、「矢印の考え」で正三角形ABCのAが移動した形で、正三角形A’ACが隠れています。
面積を求めるには、関係する部分の辺の比が分かりたいです。
ただ、この図形の中だけでは、問題を解くために必要な相似形が見えてきません。
与えられた図形の外に飛び出して「新しい図形」を自分で作りましょう。
「補助線=線を延長」して相似形を作る：図形を少しずつ解明する姿勢
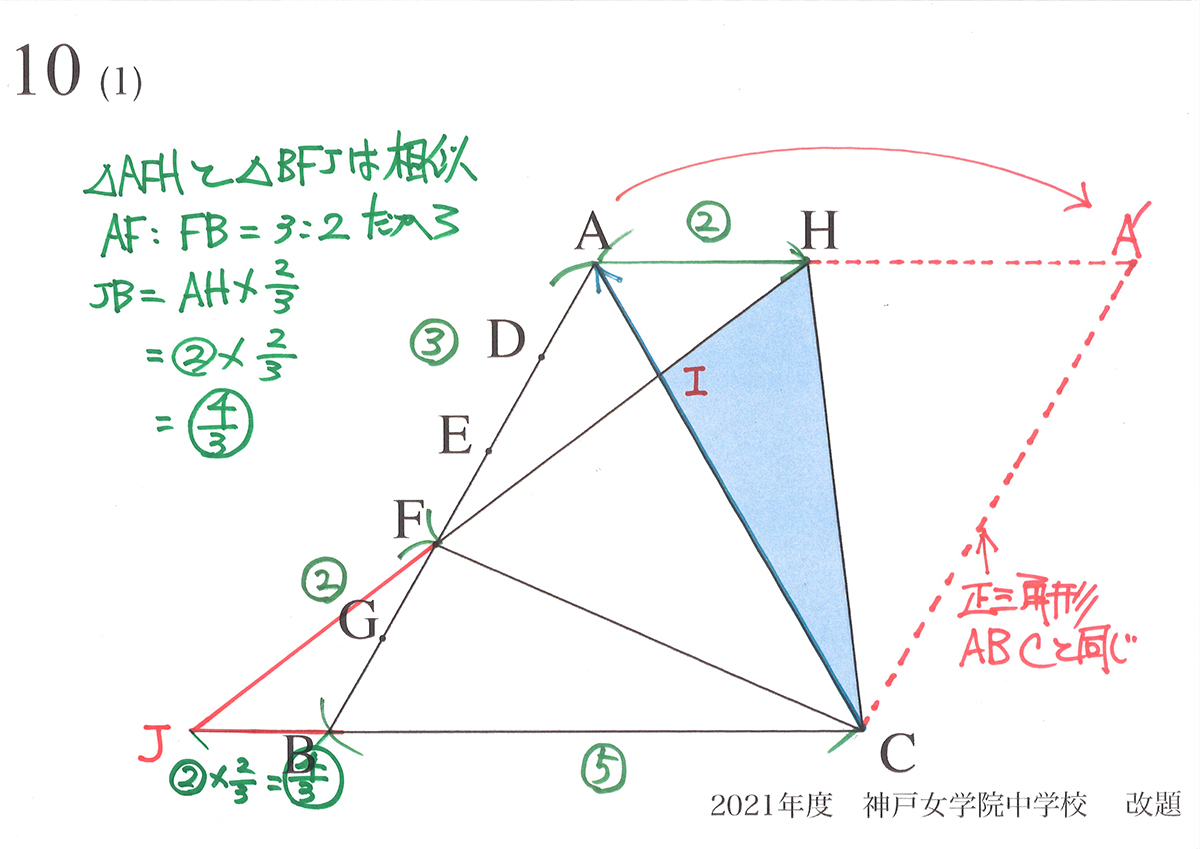
HFを延長して、CBの延長線との交点をJとしましょう。
これで、様々な相似形が見えてきました。
ここから、面積を求めるにはいくつか方法があります。
「△AHCは△CBFと同じ（合同）」ですから、△AHCの面積は分かります。
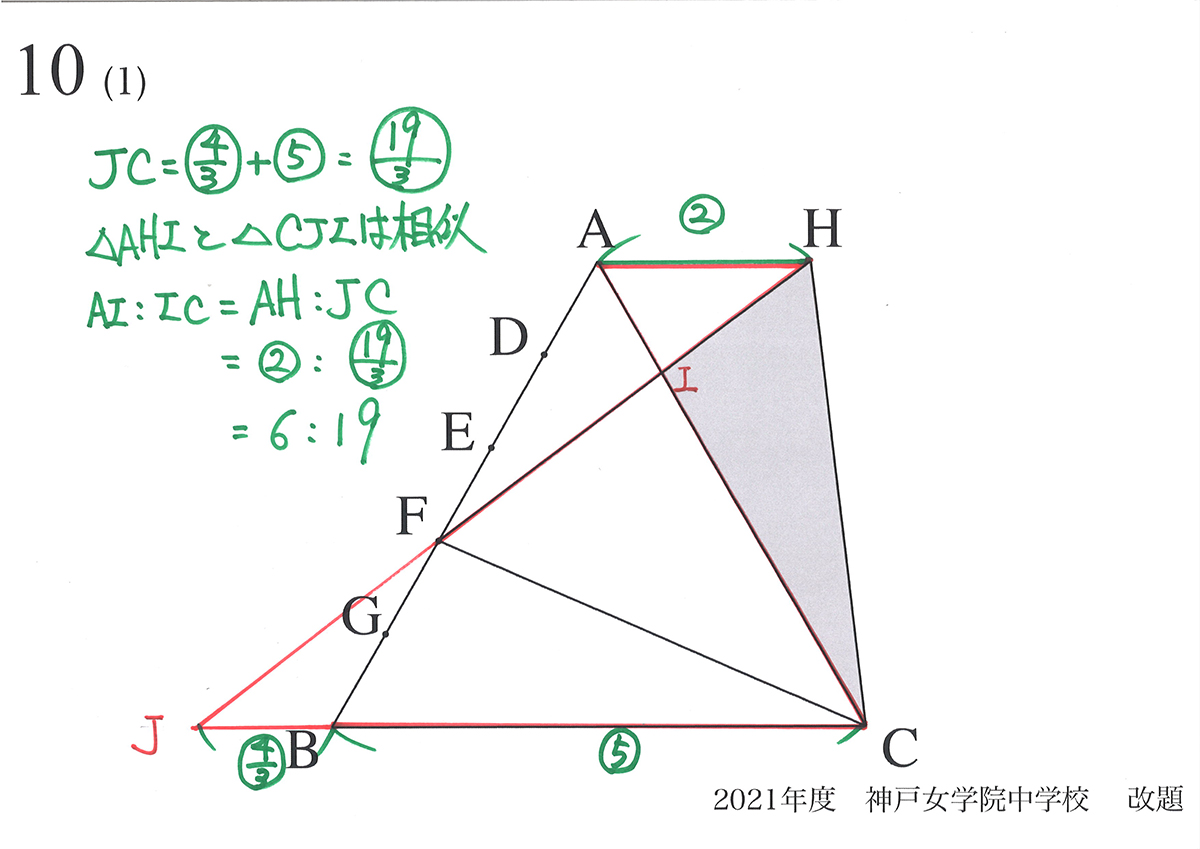
ですから、AI : IC を考えましょう。
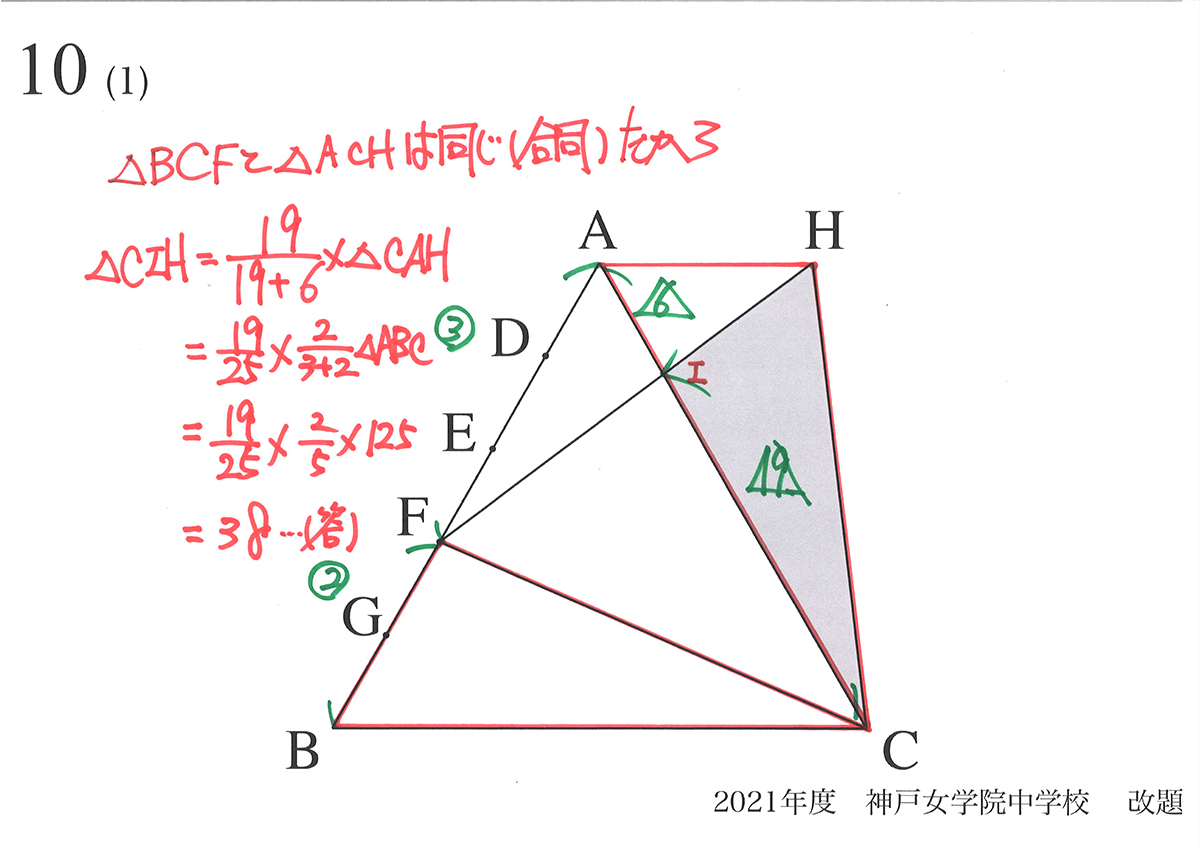
これで、面積は求まります。
計算過程を明確に：しっかり理解力アップ
「面積=辺の比」を使うときは、特に記述式ならば、上記のように「辺の長さの和」の計算を書くと良いでしょう。
万が一計算ミスをしてしまった時、あるいは「途中で終わってしまった時」などでも、採点者に
ここまで、
僕は分かっているよ！
とアピールできます。
学校の教育理念・カラーにもよりますが、「学力があること」よりも「しっかりと考えられること」の方が大事です。
また、こう言う式を書くことで、
丸暗記ではなくて、
意味が分かって解いています！
と、表現することになります。
採点者からみると、こういう答案の方が「好感が持てる」のです。
しっかり、
理解できているね！
「考えていること」はハッキリ・きっちり書くように日頃から練習しましょう。
別に「3+2」とか、
すぐ分かるし・・・
と、思うかもしれません。
この「3+2」をあえて書くと、「比と面積の関係」がしっかり理解できるようになるでしょう。
こういうことを「しっかり書く」と図形問題の理解も進み、応用力が増強されます。
