前回は「算数の効果的勉強法〜「分かった気になる」ではなく「しっかり理解」・理解して「再現する」学び・「略して書く」勉強方法・思考の流れを整理〜」の話でした。
思考する領域が広すぎる「中学受験の算数」:多数の学ぶ分野

今回は、中学受験算数で少し伸び悩んでいる方、思うように点数が上がらない方向けの話です。
少し基本的な話が中心になります。
そのため、ある程度算数が得意な方にとっては「当たり前のこと」かもしれません。
算数実践では、中学受験の過去問を中心に問題をご紹介しています。
中には、僕が改題した問題やオリジナル問題などもあります。
中学受験の算数の問題は、非常に多岐に渡ります。
中には、もはや「算数の領域」を完全に超えている問題もあり、「算数とは別」と考えられます。
「中学受験の算数」と「大学受験の数学」を比較するとき、後者の方が難易度が高いのは当然です。
一方で、ある見方をすれば、「中学受験の算数」は「大学受験の数学」より思考領域が広いとも言えます。
 男子小学生
男子小学生えっ?
大学受験の数学より「広い」の?



それじゃ、問題が
解けるようにならなくても、仕方ないか・・・
このような声が聞こえてくるかもしれませんが、「一つの見方」であり、実際に難しい問題が多いです。
「大学受験の数学」には多数の問題がありますが、「数学的思考」の領域は「通常の思考範囲内」です。
一方で、「中学受験の算数」は「通常の小学校の算数」の領域を「明確に逸脱している」問題が多いです。
中には、



この問題を
小学生に解くことを求めるのか・・・
「ちょっと行き過ぎでは」と感じる問題もあったり、



これはちょっと
難しすぎるのでは・・・
「小学生には難しすぎでは」と感じてしまう問題も見かけます。
そして、「中学受験の算数」には実に多数の分野や考え方があります。
計算方法としては、基本的に四則演算ですが、図形・比・ニュートン算・旅人算・場合の数・・・
実にたくさんあって、基本的にこれら全分野を学ぶ必要があります。
「大学受験の数学」には、微分積分・ベクトル・数列・二次方程式・・・と多数の分野があります。
これらの多数の分野は、「根本的考え方が異なる」場合が多いです。
「中学受験の算数」では「根本的考え方が異なる」場合もあります。
一方で、「中学受験の算数」は「横断的考え方」が多いとも言えます。
例えば、「図形と場合の数」は全然違う分野ですが、「比とニュートン算」は類似性が強いです。
このため、「中学受験の算数」では、分野を分けすぎない学び方が良いでしょう。
算数の理解力をアップする学び方:「考える対象」を絞る思考法


文章題の問題で、具体的に考えてみましょう。
上記問題を題材とした「てんびん算」を解くコツを、上記リンク以降でご紹介しています。
この問題は「難易度が高い」問題で、難しい理由がいくつかあります。
・問題文が比較的長いので理解するのが難しい
・「半分の食塩水」の正体が理解しにくい
・対象がA,B,Cの三つがある
この問題がサラサラ解けるかたは、相当に「中学受験の算数」が得意な方でしょう。
上記の三つもの「難しい理由」があります。
この問題を見て、



この問題は
無理だよ・・・



ちょっと
難しすぎて・・・
こう感じる方も、いらっしゃるかもしれません。ここで、
下記の問題を考えてみましょう。
太郎くんと次郎さんは、ノートと鉛筆を買いに文房具店に行きました。
太郎さんは、ノート2冊と鉛筆3本を購入したら570円でした。
次郎さんは、ノート5冊と鉛筆7本を購入したら1380円でした。
ノートと鉛筆の値段を求めて下さい。



この問題なら
すぐに出来るよ!



これなら
簡単!
この問題は、中学受験生の多くの方が解けるでしょう。
解説は略しますが、ポイントは「未知数を設定(①など)して、消去する」です。
「消去算」と紹介されていることもありますが、とにかく基本は「立式すること」です。
そして、この問題を解く際には、大事な視点があります。
それは、「どちらかに注目すること」です。
ノートと鉛筆の両方を相手にしていては、なかなか解けないです。
そこで、「考える対象をどちらかに絞る」のが非常に重要です。
・問題文の状況に合わせて未知数設定して、立式
・まず「考える対象を一つに絞る」
消去算の根本的思考は「考える対象を減らす」ことです。
上の問題で、鉛筆とノートに加えて、消しゴムなどが加わると少し難易度が上がります。
この時、同じように「考える対象を絞ってゆく」思考が大事です。
様々な分野の問題がありますが、「考える対象を絞る」思考法は常に意識しましょう。
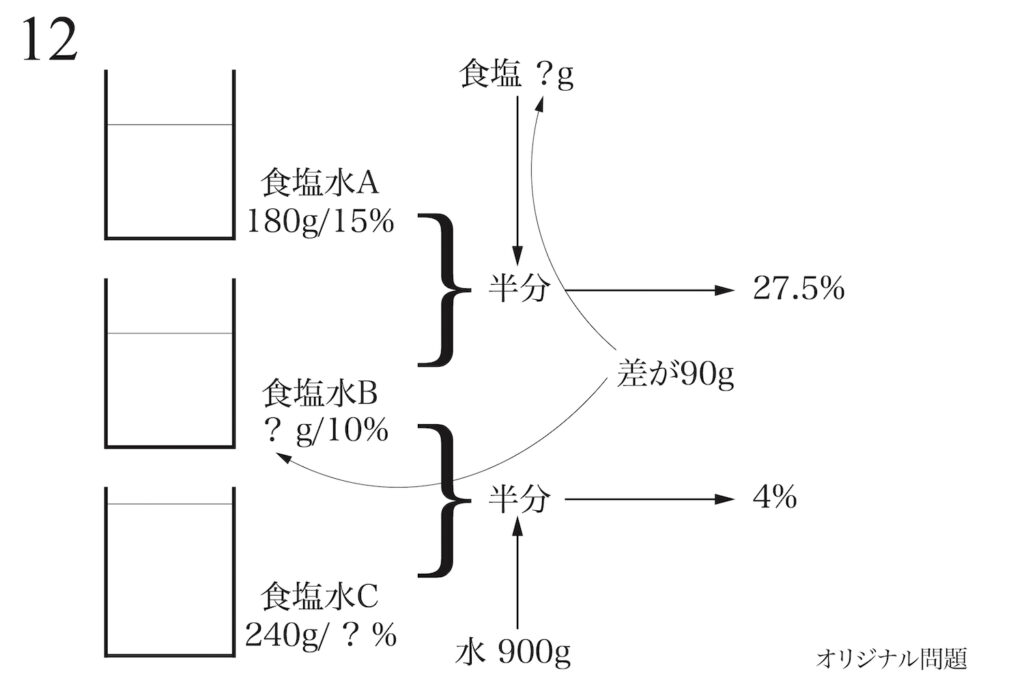

上記の食塩水の文章題のように「長い文章題」に出会ったら、簡単なメモを書くのが良いでしょう。
・状況を簡単な絵や図に描く(状況の整理)
・大事な量や長さなどを見落とさない



別にこの図を描かなくても、
内容は分かっているけど・・・
「描かなくても分かる」という方もいらっしゃるかもしれません。
特に文章題では、「状況の整理」は文章題では最重要です。
そして、この問題のように「A,B,Cの三つが登場する」問題は、「どれかに注目する」姿勢が大事です。
難しい問題が多い「中学受験の算数」ですが、「考える対象が4つ以上」という問題「ほぼない」です。
「考える対象が3つ」と「考える対象が2つ」では、問題の難易度が格段に上がります。
それは、「対象を絞る」プロセスで「何かと何かを比較する」ことがあります。
この時、「考える対象がAとB」ならば、比較するのは「AとBしかない」状況です。
一方で、「考える対象がAとBとC」ならば、比較するのは「AとB」「AとC」「BとC」の三つがあります。
・どれか一つを中心にする
・三つを一度に相手にせず、ある二つの量を比較
てんびん算でも旅人算でも、「比較する」ことは大事な考え方です。
多数の分野がある「中学受験の算数」において、「分野ごとの攻略」も良いかもしれません。
一方で、「考える対象を絞る」と「何かと何かを比較する」という基本を意識すると良いでしょう。
・考える対象を、どれか一つに絞る
・何かと何かを比較してヒントを得る
そして、そもそも「何を求めるのか」や「何を中心に考えればよいか」を考えてみましょう。
「とにかく多くの問題を解く」よりも、ポイントを明確にする思考法の方が算数は学力が上がるでしょう。
次回は上記リンクです。



