前回は「電気・電流・回路の分かりやすい考え方 2〜回路に流れる電流・全体の流れを描いて考える・電池一つの電圧に対して流れる電流=①・比較する大きさを設定・分かれる電流はどちらに流れる？・電流同士が衝突？・仮に流れる向きを考える・具体的にイメージ〜」の話でした。
分からない電流と未知数：分かるところから考える姿勢
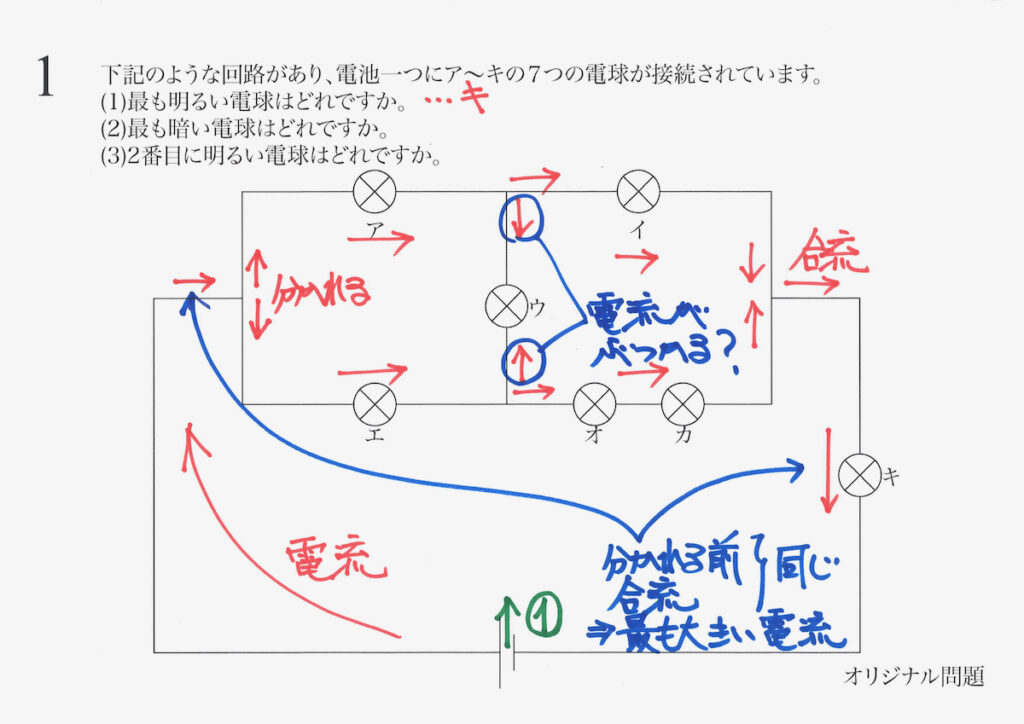
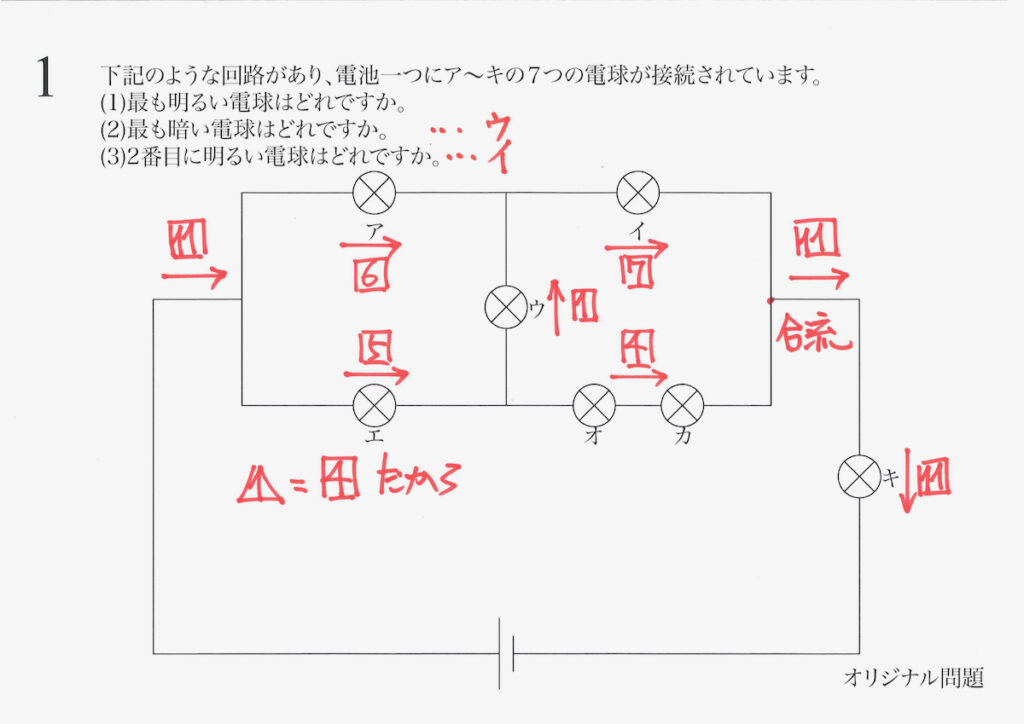
中学受験の電気の問題で比較的よく見かける「明るい電球」を考える問題。
電気の問題は、いくつかの回路を考える問題、文章題で複雑にした問題などあります。
てこ、ばね、かっ車などの問題も同様ですが、「基本を押さえれば、全て出来る」ようになります。
まずは、「電流の流れ・分流と合流」を考えて、最も明るい電球が分かりました。
理科・社会などで「分かることから、少しずつ考えてゆく」姿勢は大事です。
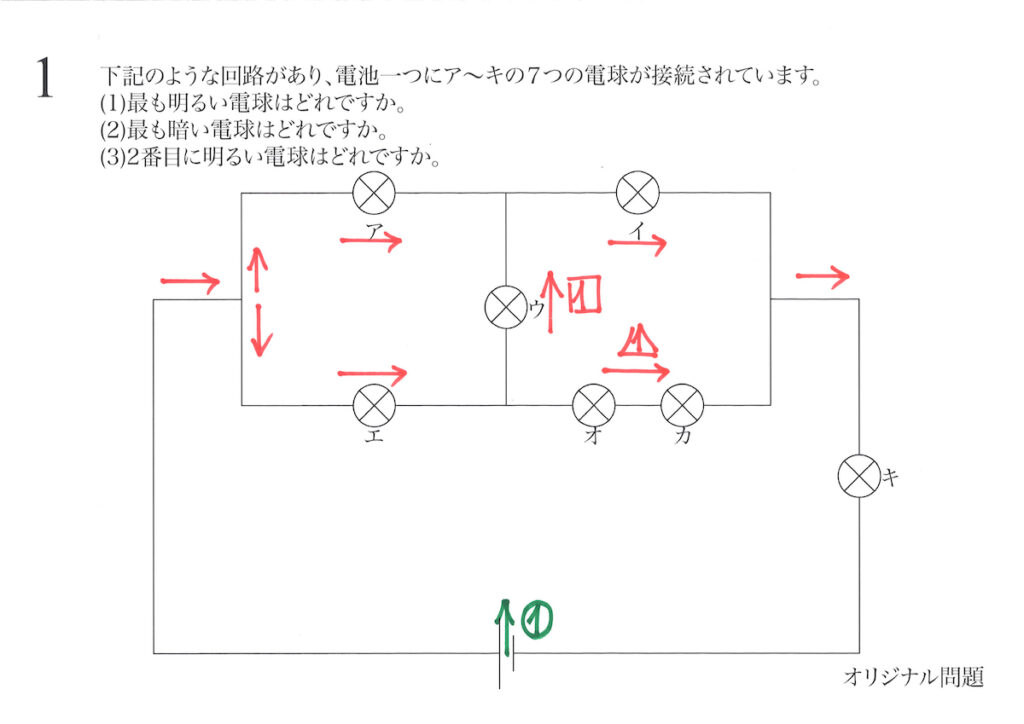
シンプルな回路に見えますが、電流が別れたり合流したりで、全体が分かりにくいです。
分からない電流の大きさに対して、それぞれ未知数を設定しました。
これで、回路全体の電流を考えてゆきましょう。
男子小学生簡単そうだけど、
難しいよ・・・
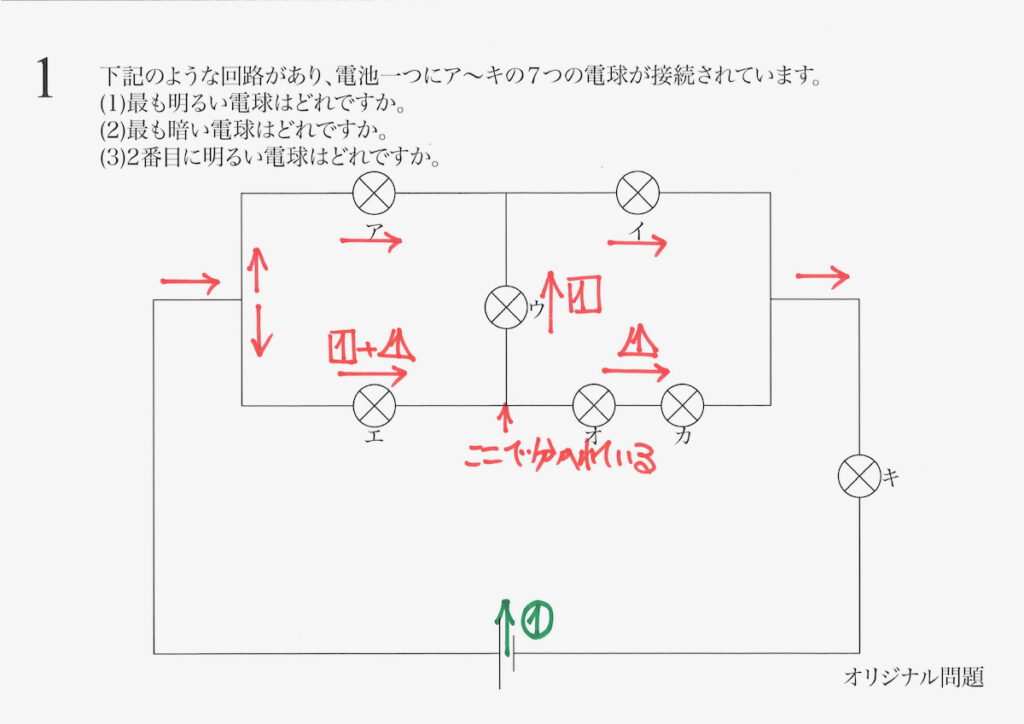
まずは、最も分かりやすい「電流が別れる前」を考えます。
こういう問題では「一気に解く」ことを考えず、分かるところから考える姿勢が大事です。
上の図の点で電流が分かれているので、エの電球を流れる電流が分かります。
女子小学生確かにここは、
分かれる前だね。
前回同様、電球一つの抵抗を「1」と考えます。
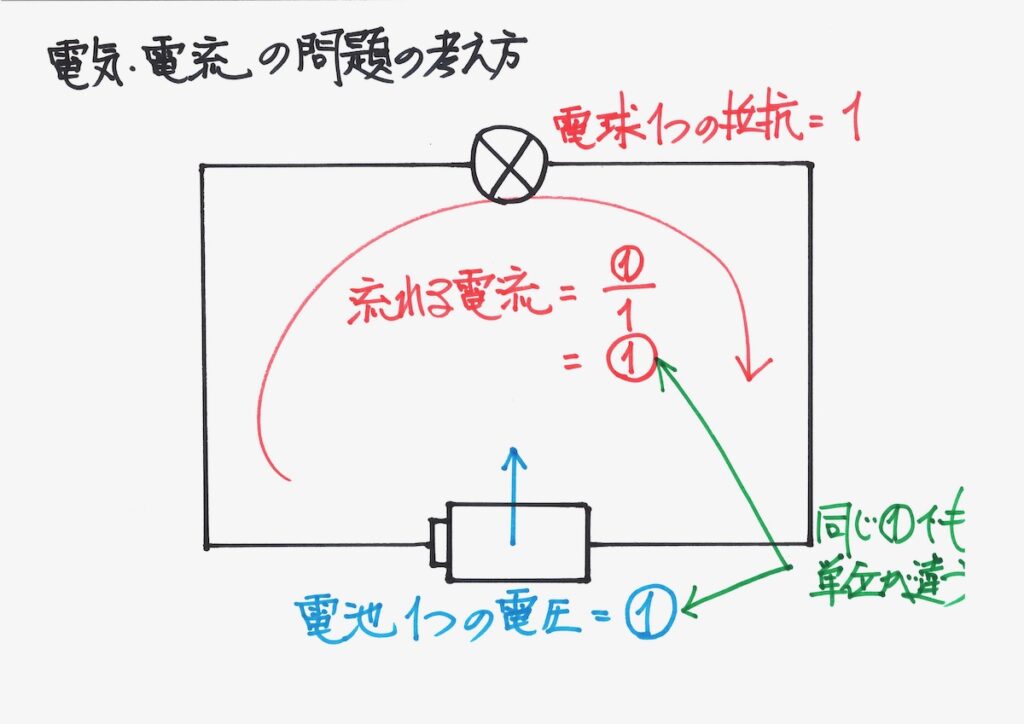
オームの法則から「流れる電流=電圧=①」となりますが、「同じ量」ではなく単位が異なります。
・電圧 = 電流 x 抵抗（オームの法則）
・主役は電圧
・「電池 = ポンプ」が回路に電流を流す
・回路を流れて、一周した電流は「上がった高さ」分下がる（電圧効果）
異なる経路の電圧が下がる大きさ：電圧降下
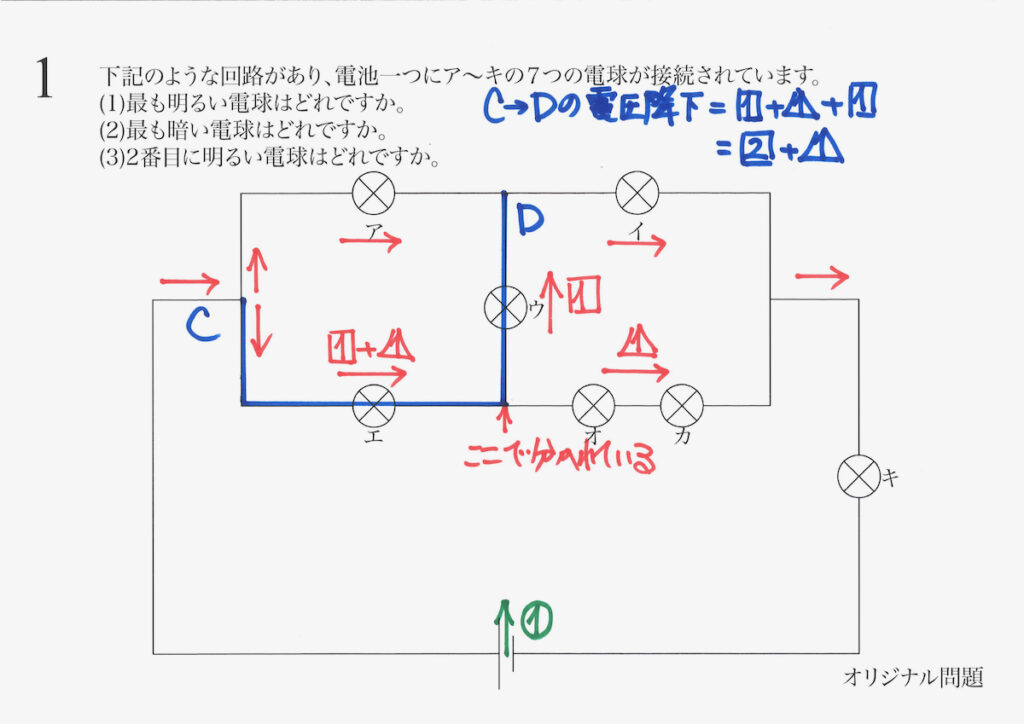
次は、上の図のC →Dの下がる電圧（電圧降下）を考えます。
電流は「電球（内部に抵抗）や抵抗を通ると電圧が下がる」のが大きなポイントです。
文字通り「抵抗を受ける」とダメージを受けるイメージです。
まずは、青色の経路で考えてみましょう。
エ→ウの順に電球の抵抗（1)を受けるので、「電圧=電流x抵抗」を計算します。
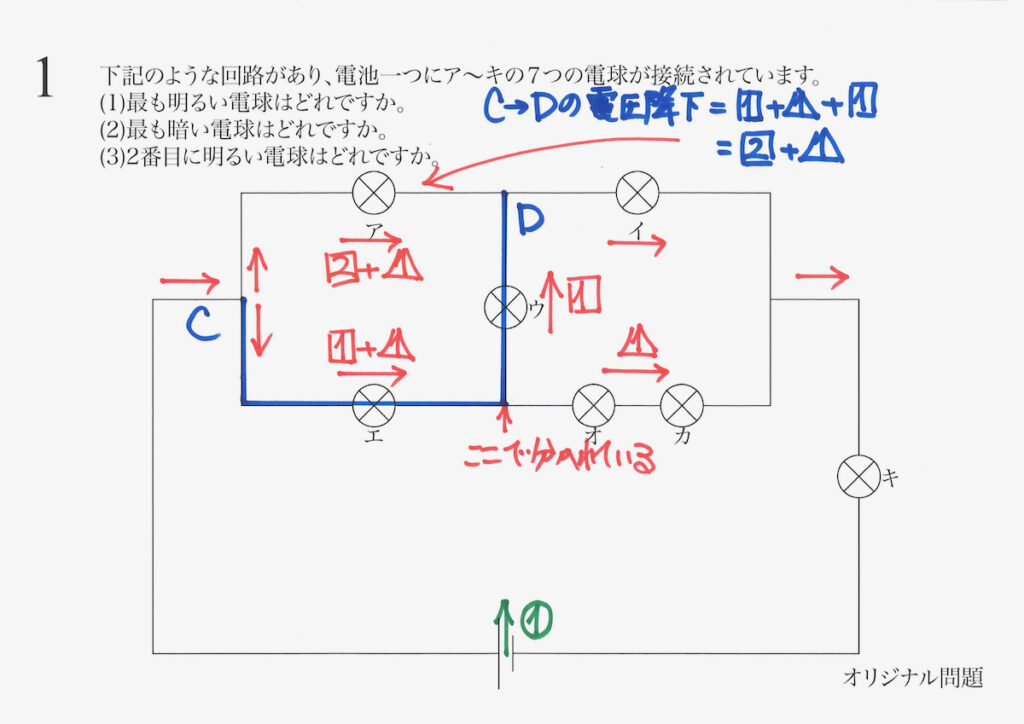
C →Dの下がる電圧（電圧降下）は、電球アを通る電流による電圧降下と同じなです。
そこで、アを通る際の下がる電圧（電圧降下）が分かり、アを通る電流が分かります。
これで、だいぶ分かってきました。
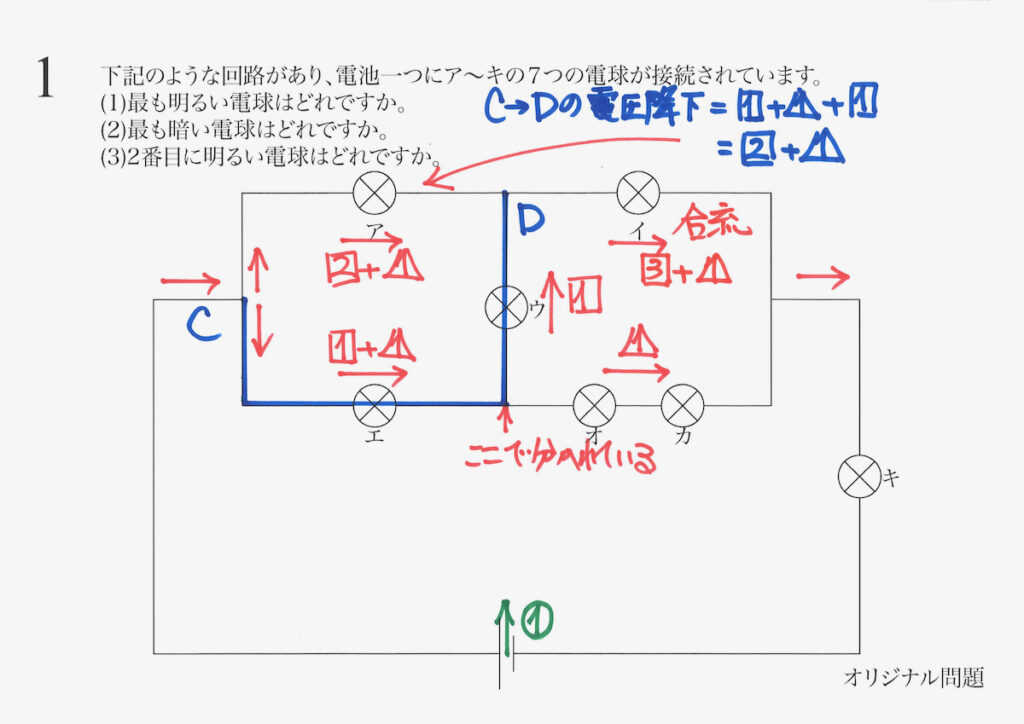
次に、Dで電流が合流するので、合計すると「電球イに流れる電流」が計算できます。
女子小学生なんだか、
探偵の推理みたいな感じだね。
推理探偵のように「少しずつ問題を解明」してゆきましょう。
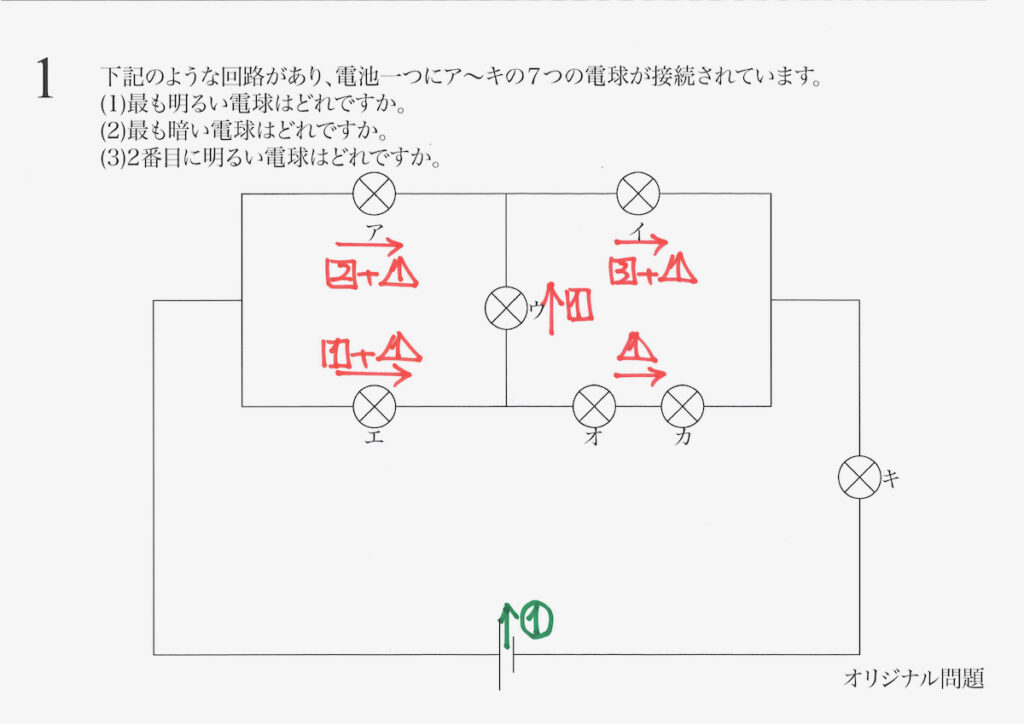
ここで、回路を流れる電流を一度整理します。
これで、シンプルだけど少し複雑な回路に流れる電流が分かってきました。
最後に、「二つの未知数の関係」を求めましょう。
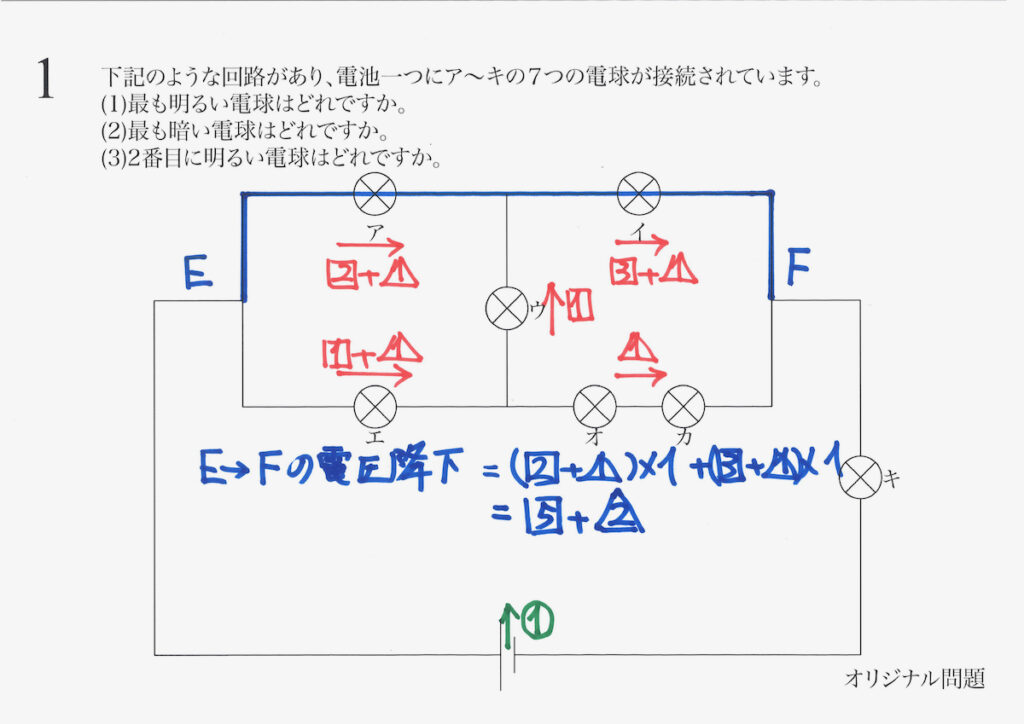
今度は、たくさんの電球があるEからFを考えましょう。
EからFで、電圧が下がります。
女子小学生この場合も
さっきと同じで、電流の経路を考えるんだね。
まずは、上の図の青色の経路を考えて、下がる電圧の大きさを「電圧=電流x抵抗」で考えます。
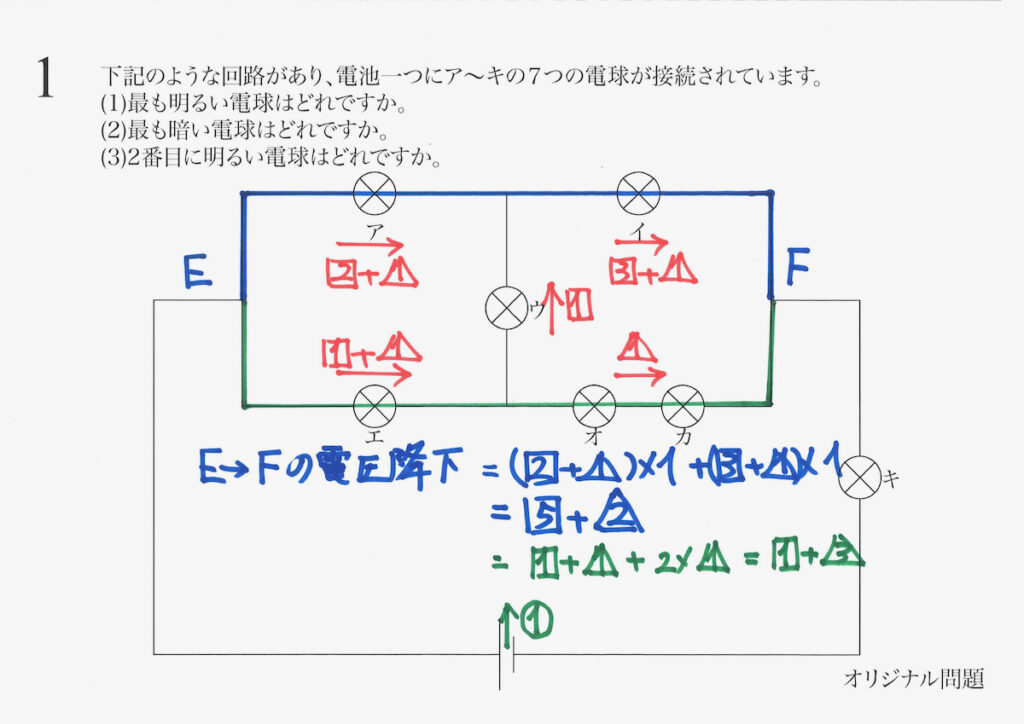
次に、緑色の経路でEからFの下がる電圧の大きさを計算します。
女子小学生この二つの「下がる電圧」は
同じはずだね。
これらが等しいので、関係式が求まります。
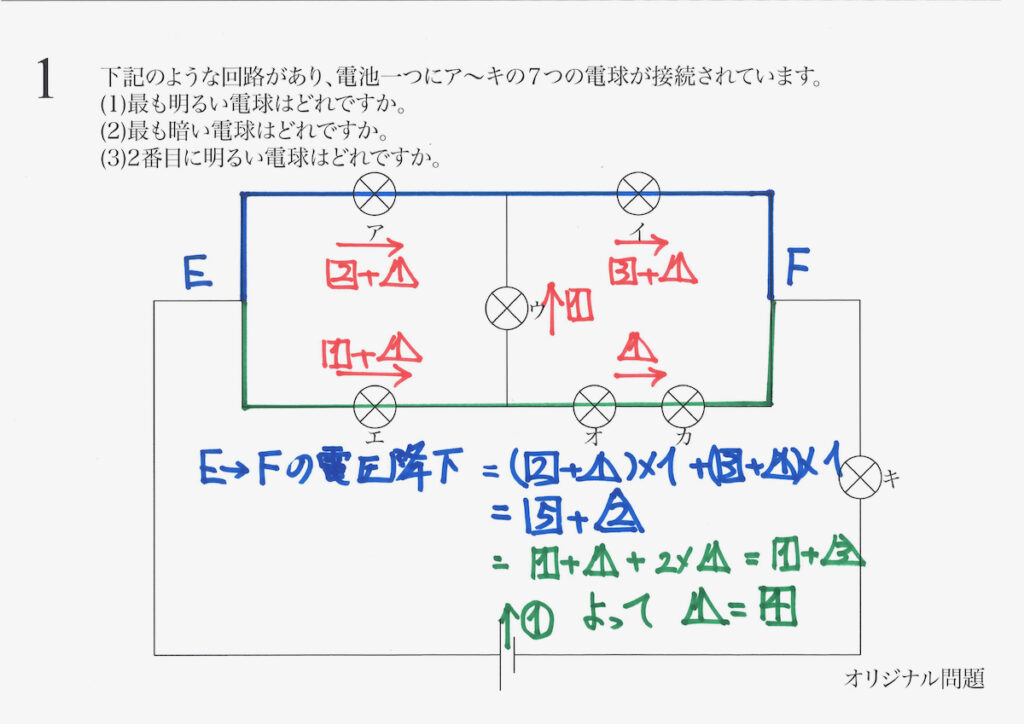
分からなかった電流の大きさの未知数の関係式が求まりました。
女子小学生未知数だった電流の
関係が分かった！
関係式を使って、それぞれの電流の大きさを描いてみましょう。
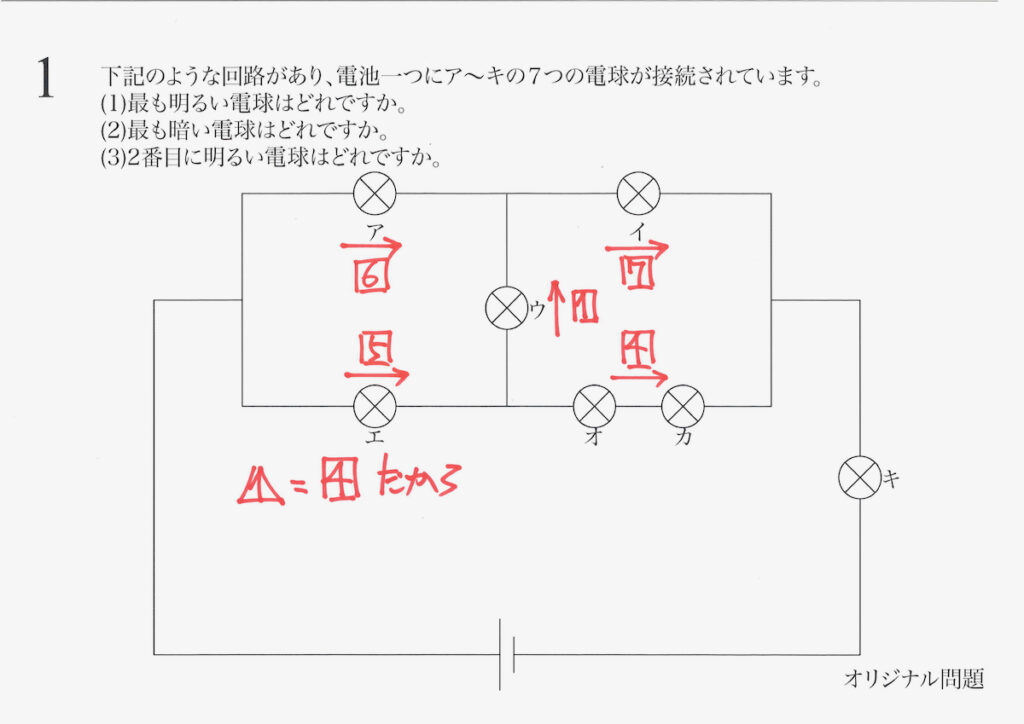
電流が別れる前、合流した後も、計算できます。
各電球に流れる電流の大きさが分かり、「電流の大きさ=明るさ」なので、答えが分かります。
女子小学生あとは、単純な
数字の比較になるね。
(2)の答え・・・（ウ）です。
(3)の答え・・・（イ）です。
どのくらいの明るさか：電流を具体的に計算
回路の全容が分かり、問題が解けました。
理科や算数の問題では、「問題が解けたら終わり！」でも良いですが、少し考えてみましょう。
男子小学生この電球の明るさは
どのくらいなんだろう？
このように「問題にないこと」を考えてみる姿勢は、とても大事です。
理科・算数で「少し横道にそれてみる」と色々なことがわかり、勉強になります。
ここで、最も明るいキの電流の大きさ・明るさを考えてみましょう。
上の基本回路の電流の大きさと比較してみましょう。
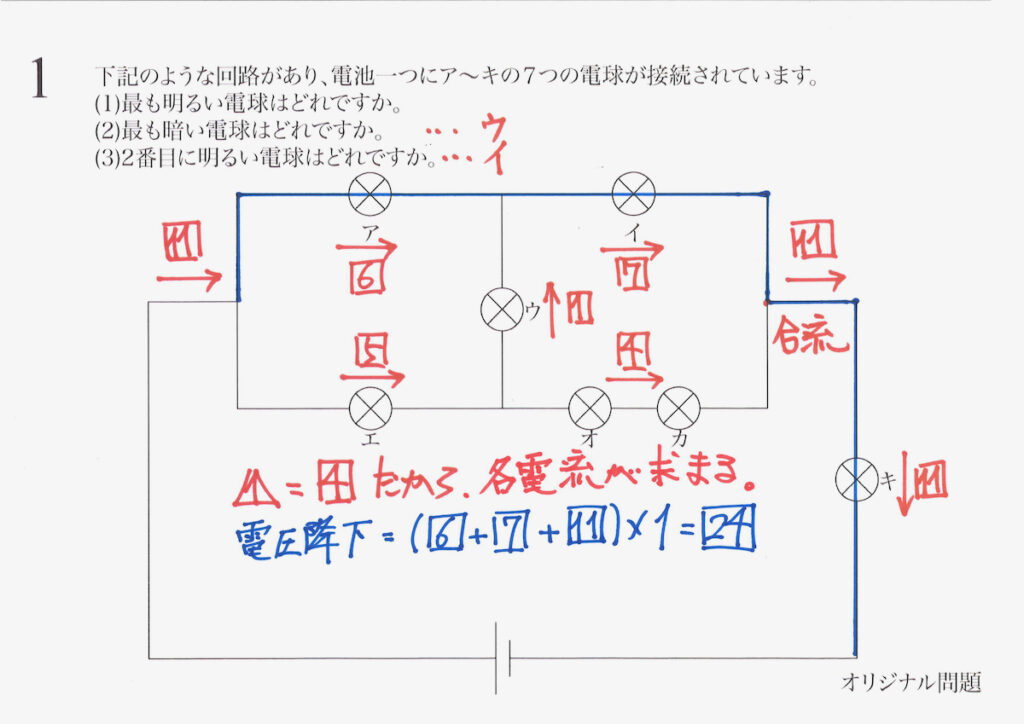
抵抗を受ける部分で、青色のルートで下がる電圧（電圧降下）を計算します。
電線の抵抗を無視するので、電池から出た電流は「電球・抵抗がない=抵抗を受けない」です。
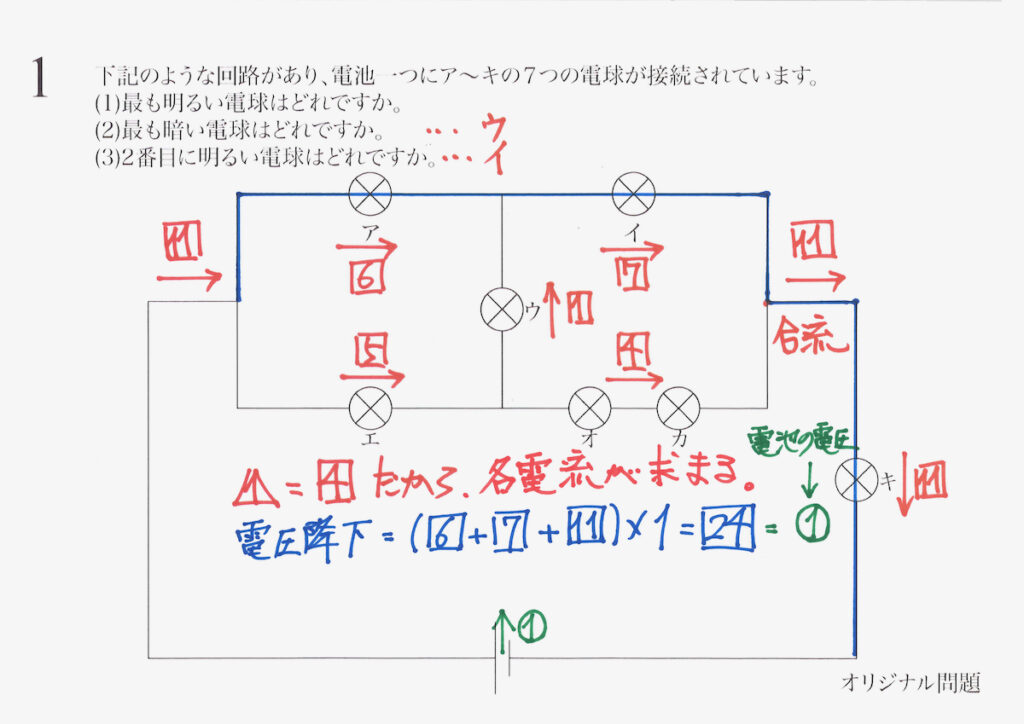
これが、電池が持つ電圧と等しいです。
男子小学生確かに
そうだね！
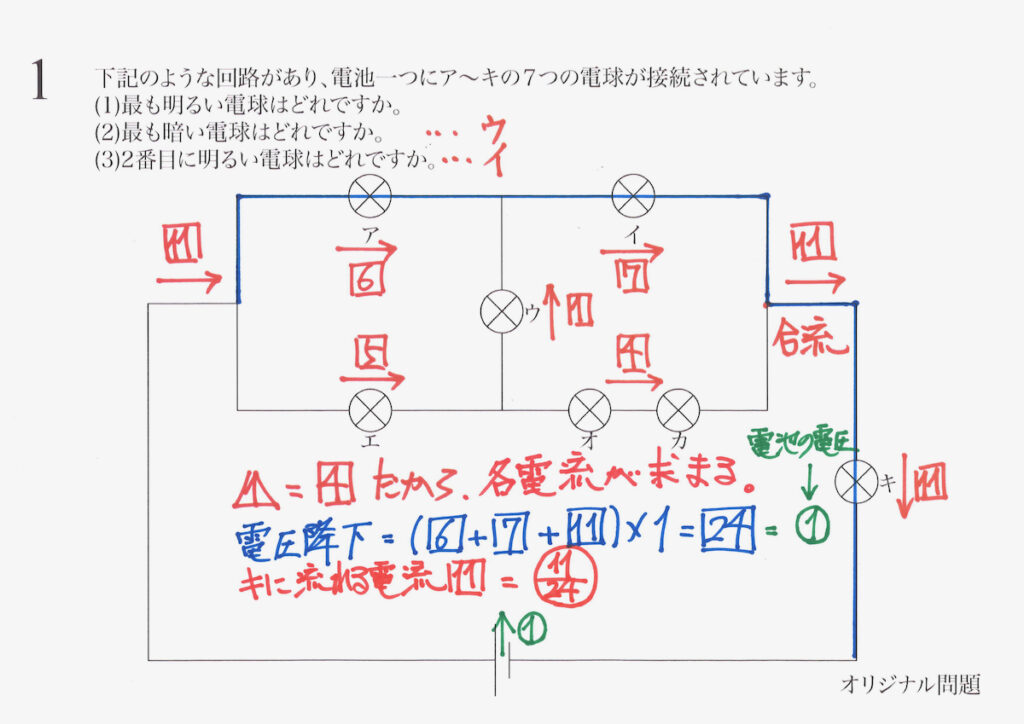
そして、キの電球を流れる電流の大きさが計算できます。
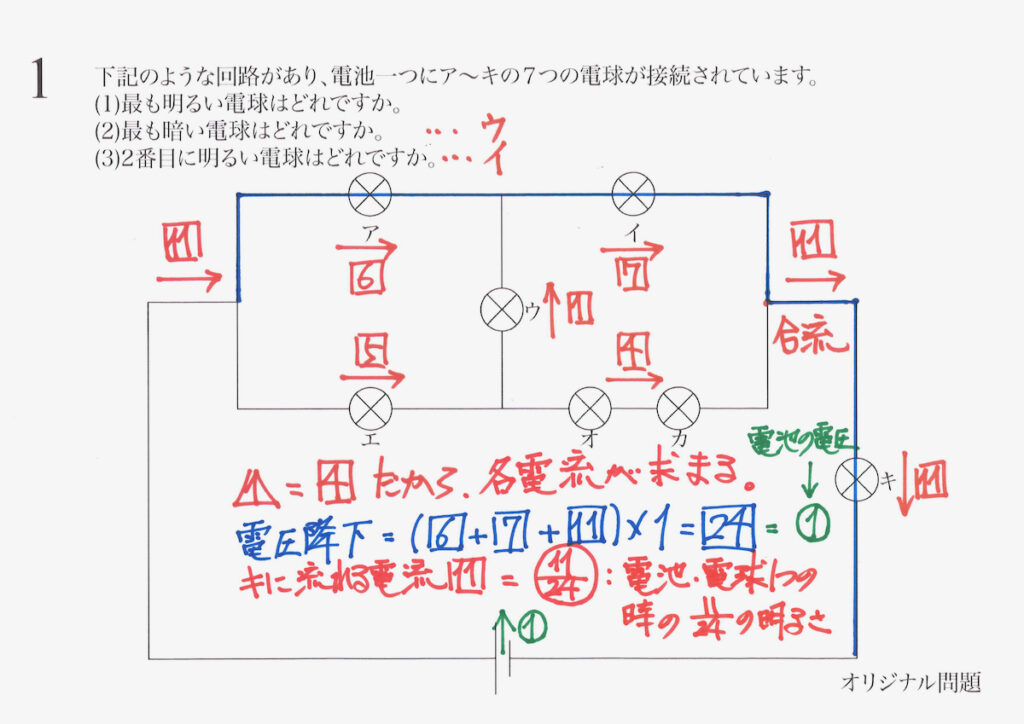
キの電球を流れる電流の大きさは、基本回路の電流の大きさの11/24です。
そして、明るさも11/24（電流と明るさが比例する時）です。
上のように、回路の電流が全て求まりました。
「点と点で下がる電圧が同じ」は、いろいろな点で確認してみましょう。
男子小学生本当だ。
ちゃんと、下がる電圧が同じ。
女子小学生確かに、
同じだね！
女子小学生なんだか
不思議な気持ち。
理科の物理の内容は、基本原理が分かれば、考え方が少し異なっても同じになります。
この「同じ結果になる」ことを色々と考えてみると、力学・電気などの理解が進むでしょう。
算数や理科で「異なる考え方」を学ぶことは、非常に大事なことです。
回路の問題は未知数として設置する「分からない電流」を違う電流にしても、同じ結果が得られます。
回路が複雑になっても、基本原理は変わりません。
基本的な原理をしっかりと理解して、イメージしてみましょう。
文章題で、様々な回路や電流計・コンデンサーなどが出ることがありますが、基本は全て同じです。
しっかりと「電圧の違い」を考えてみましょう。
その「しっかり」の姿勢で、電気・電流の問題は出来るようになるでしょう。
次回は下記リンクです。
