前回は「てんびん算のコツ・食塩水の問題・解き方 3〜「なぜ?」と釣り合い・バランス・比・濃度・量・難しいことは分割して考える・「混ぜる」を描いて理解する・状況・現象に対する直感を大事に〜」の話でした。
食塩水が3つ以上の「てんびん算」
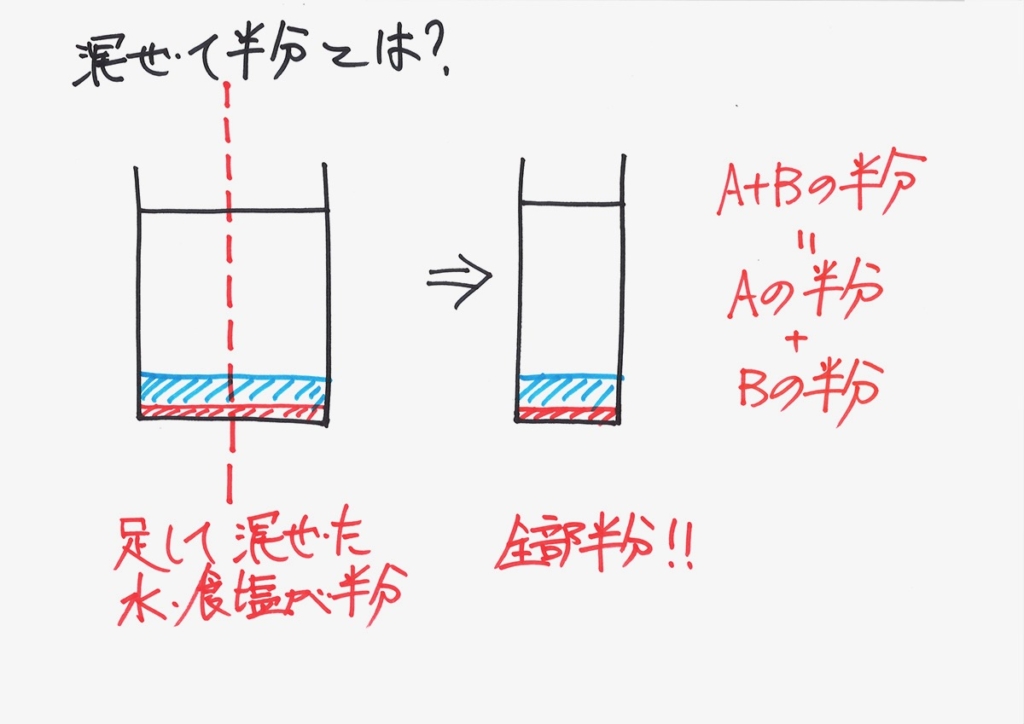
この問題の最も本質で大事なところである、「混ぜて半分」が理解できました。
この問題の良いところは、「算数と理科の両方にまたがる」ことです。
そして、「食塩水を混ぜる」ことは、日常生活では「なかなかしないこと」ですが、イメージがしやすいです。
理科実験でもなければ、日常生活で「何かと何かを混ぜる」ことは少ないです。
一方で、「何かと何かを混ぜる」と「何かが生まれる可能性がある」ので、非常に大事なことでしょう。
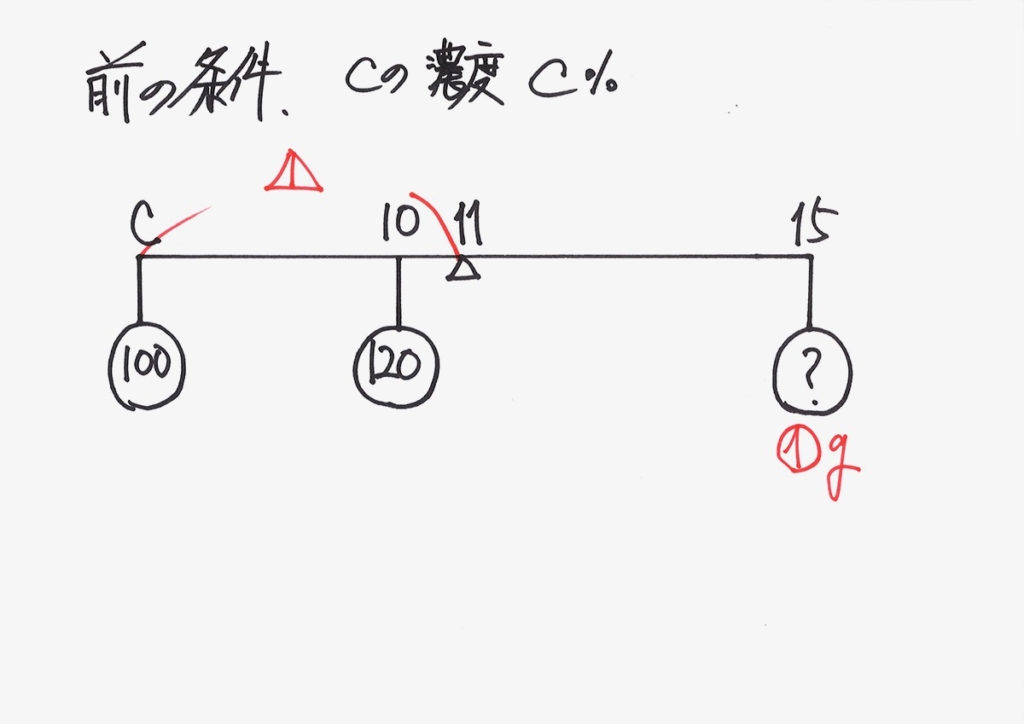
てんびんのイメージが出来たので、立式してみましょう。
食塩水が3つだと、
難しそう・・・
あまりやったことが、
ないから・・・
てんびん算・てこの原理は、「おもりがいくつになろうと同じ」です。
そこで、食塩水が3つ、あるいはそれ以上の問題があっても、
同じように考えれば
良いんだ!
と考えるようにしましょう。
未知数設置のコツ:計算を簡単に
Bの量・Cの濃度を未知数で考えましょう。
ここでは、「Cの濃度と11%の差」を未知数とします。
え?なんで?
Cの濃度を未知数にするんじゃないの?
それでも良いですが、「差を未知数」にした方が、「計算が簡単だから」です。
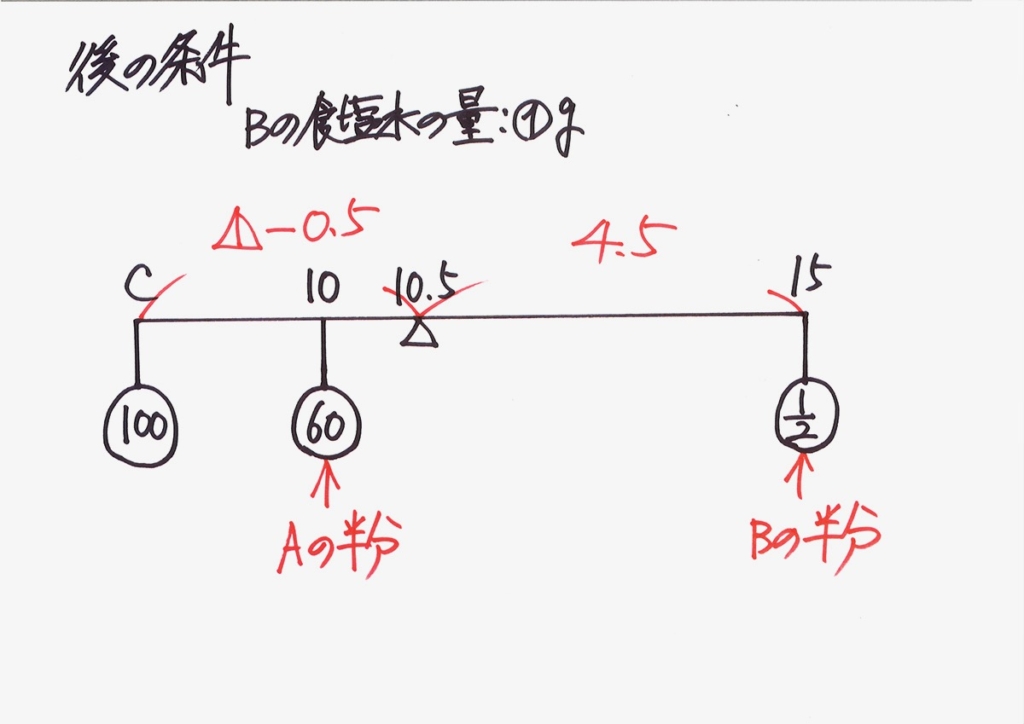
後の条件は、上のようになります。
ここからは、バランスとって、立式してゆきましょう。
支点の左側と右側の釣り合いは、「重さx長さ(支点からの距離)」です。
確かに、Cの濃度と11%の差を未知数とした方が、
計算が楽かも・・・
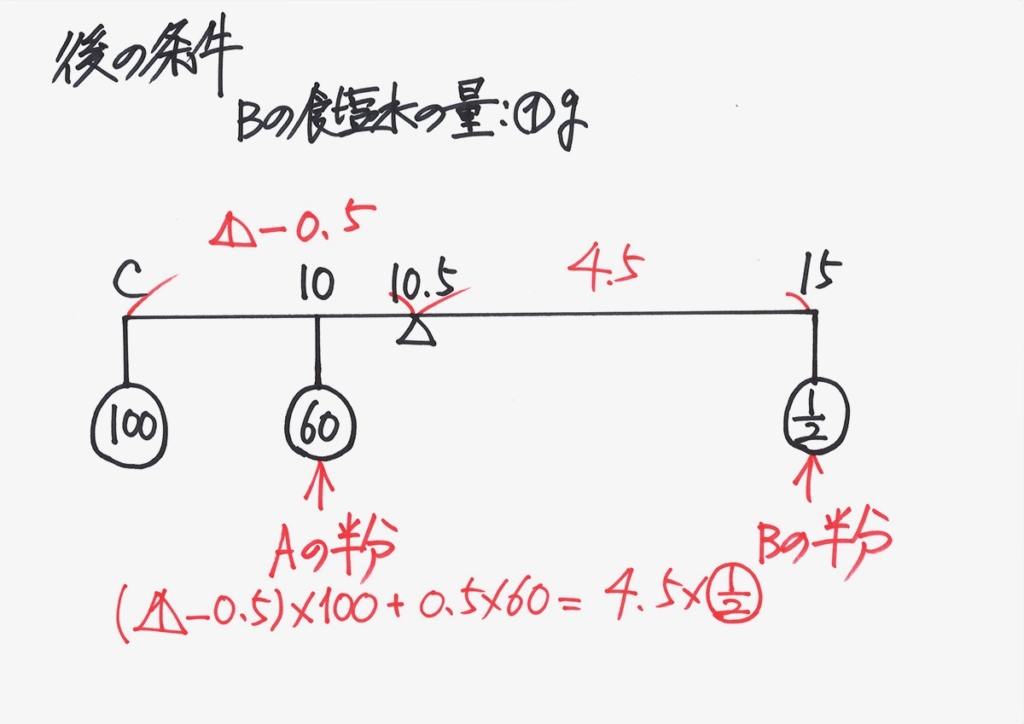
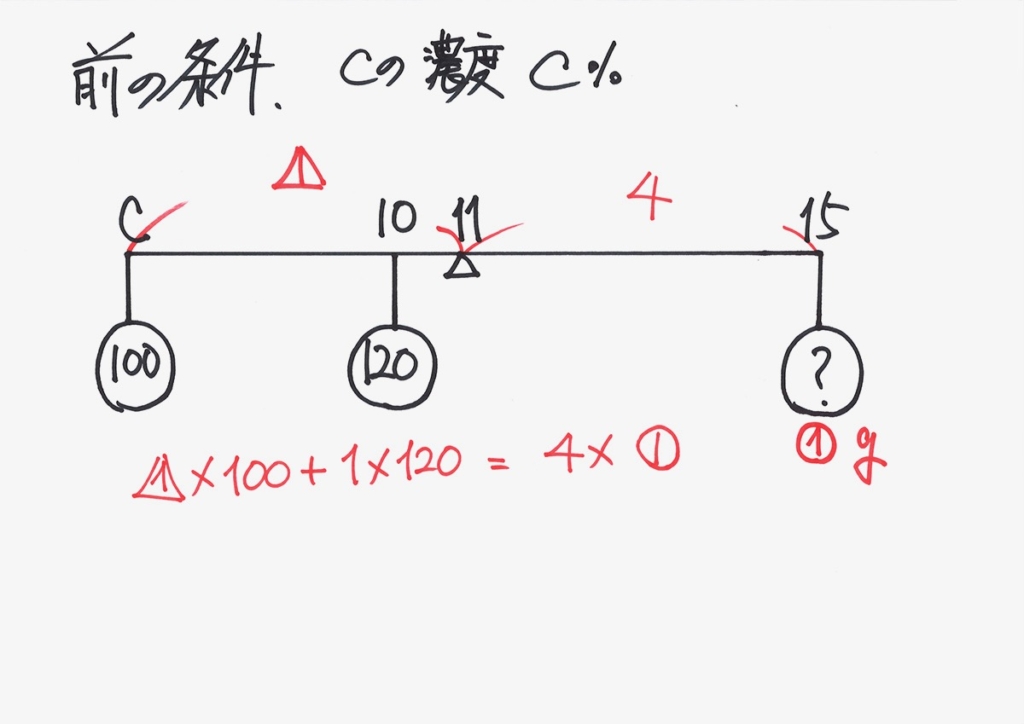
二つの未知数に、二つの(独立した)条件式が出たので、解けます。
計算ミスを防ぐ姿勢:「同じものはないかな?」

この数式を解くだけですが、こういう時は「同じものがないかな?」と考えましょう。
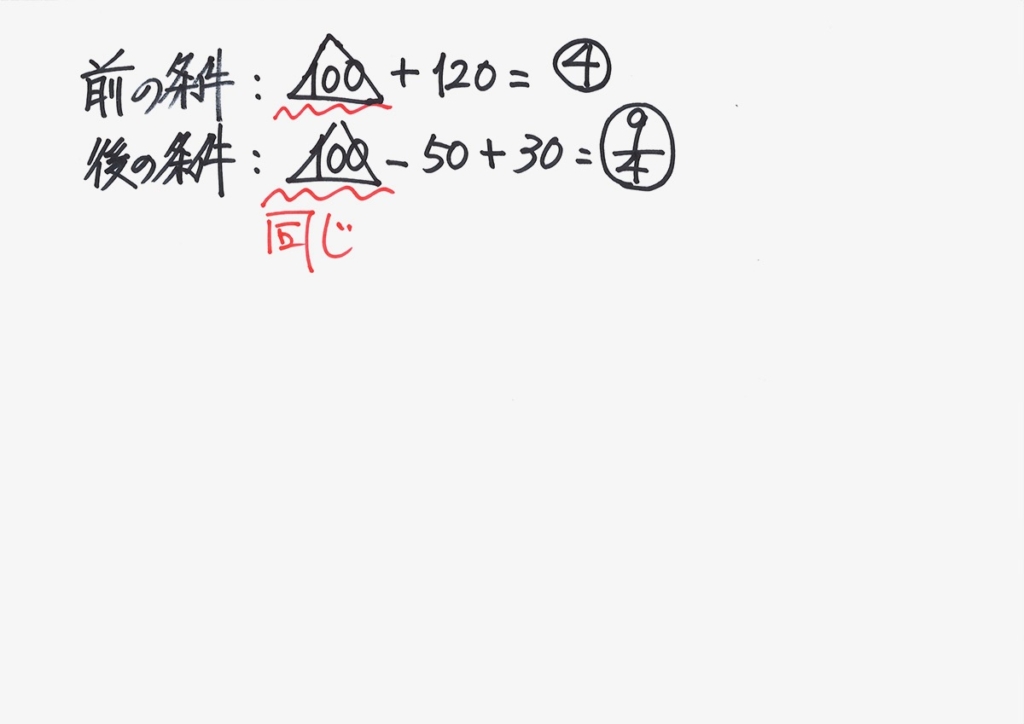
同じものがあると、計算が楽です。

辺々引くと、同じものは消えます。

Bの量・Cの濃度が求まりました。
てんびん算って、
便利だね。
解いてて、
イメージ出来るから、楽しい。
「中学への算数」では、方程式的視点で考えています。
両方の視点で出来るようになると、「多角的視野」が広がるでしょう。
方程式のみで立式すると、計算が複雑になる傾向があります。
試験の時、複雑な計算式を解くと、間違える可能性があります。
出来るだけ「計算が簡単に」なるように考えましょう。
それには、日頃から「多角的視点で考える」ことが大事です。
記事とは異なる、てんびん算の解き方をご紹介しました。
これは、著者の方の考えに対する異議ではありません。
「こういう考え方もできるよ」という、一つのご紹介です。
記事が多角的視点を提示しており、様々考えを執筆されている著者の方には敬意を持ちます。




