前回は「時間と距離の比を合わせて考えるコツ〜問題の視点を変える発想・「時間の起点」を変える・大事な「普通の」解き方・20(2)解法A〜」の話でした。
速さと比の出題が多い理由：作成しやすい「様々なシーン」
25Speed204ts
算数実践の問２０の問題は、「時間の起点を変える」発想が大事でした。
速さや比の問題は、中学受験の算数では超頻出です。
この「速さや比の問題」が多い理由は、下記が考えられます。
・「比の概念」が算数や数学の根幹の一つなので、算数の学力を測るために大事
・問題を作成するのが比較的容易
問題を作成する人は、数学科の教員が多いので「数学のプロ」です。
「数学のプロ」から見れば、「算数の問題を作成する」のは簡単そうですが、
出題者今年は、どのような
問題を出題しようかな・・・
出題者このテーマを
こんな感じで出題したら面白いかな・・・
算数の出題者たちは、「算数が好き」なので、問題の作成を楽しみながらも、
出題者算数の発想で解けるように
したいから、ちょっとこうした方が良いかな・・・
かなりの時間とエネルギーを注いで、問題を作成していると思います。
出題者やっぱり、比の問題は、
作成しやすいし、特徴を出しやすい・・・
「速さ・比の問題」は、何らかのシーンを考えれば特徴を出しやすいので、出題が多いのでしょう。
算数の学力を大幅アップする学び：「比の問題」と図形問題の類似
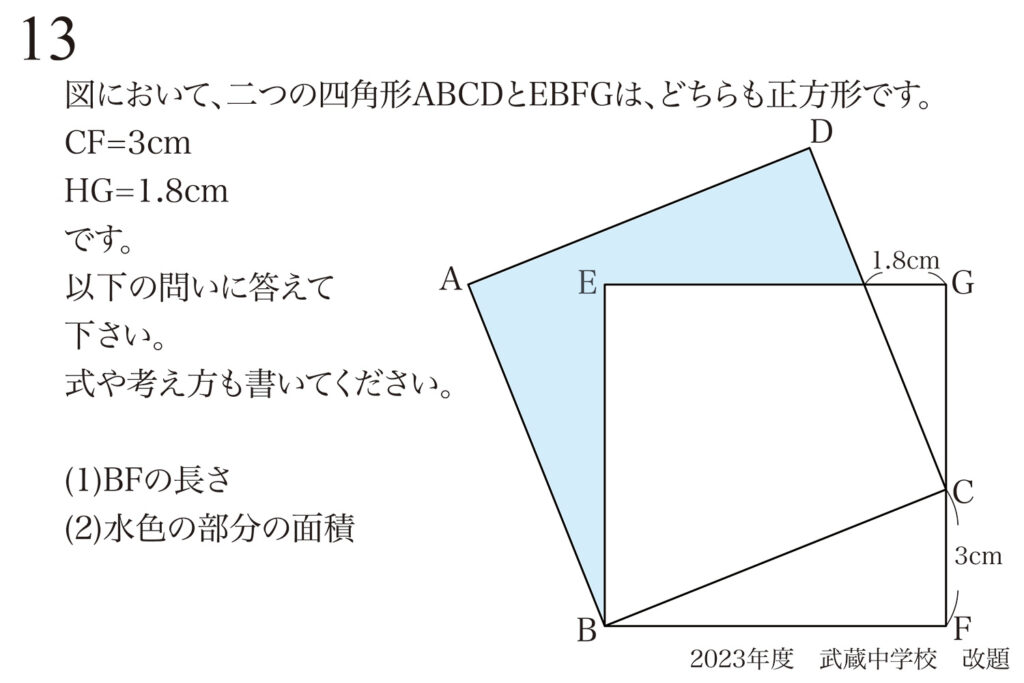
図形問題では、ほとんどの場合で「相似比」を考えて解きます。
相似比を考える際には、「まずは問題文の条件の図形を分析する」姿勢が大事です。
・問題の条件を全て描きこむ：同じ長さ・同じ角度など
・図形の性質などを描く過程で、条件を頭で整理するので解きやすくなる
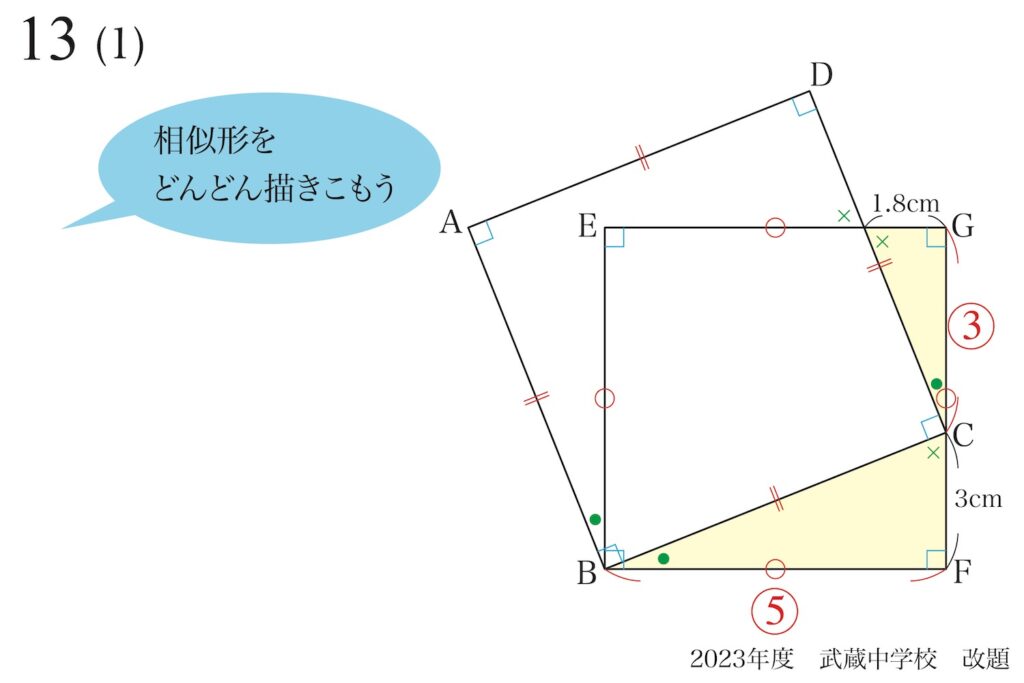
すると「相似形が見えてくる」ことがあり、問題を解く鍵が見つかります。
この問題の（１）を解く考え方を、上記リンクでご紹介しています。
この問題のように「斜めの正方形」がある時は、「外部に正方形を作る」のが一つの定石的発想です。
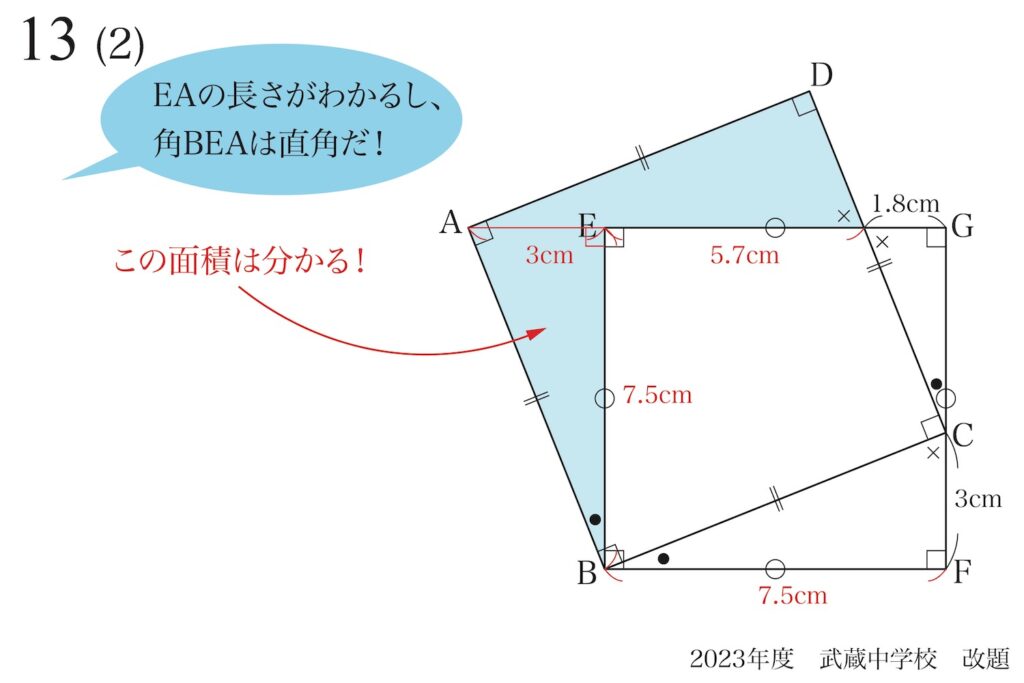
それに対して、筆者は「図形を分解・分析して解く解き方」を、上記リンクでご紹介しています。
「斜めの正方形の時は、外部に正方形」は、確かに有効な発想ですが、
男子小学生よしっ、斜めの正方形だから、
それを囲むように正方形を作る！
このように「パターン化」の発想で学ぶと、図形問題の本質が見えなくなる可能性があります。
図形問題の基本は、「対象とする図形を分析する」ことです。
その分析のプロセスで「相似や合同の図形を発見する・作る」姿勢が大事です。
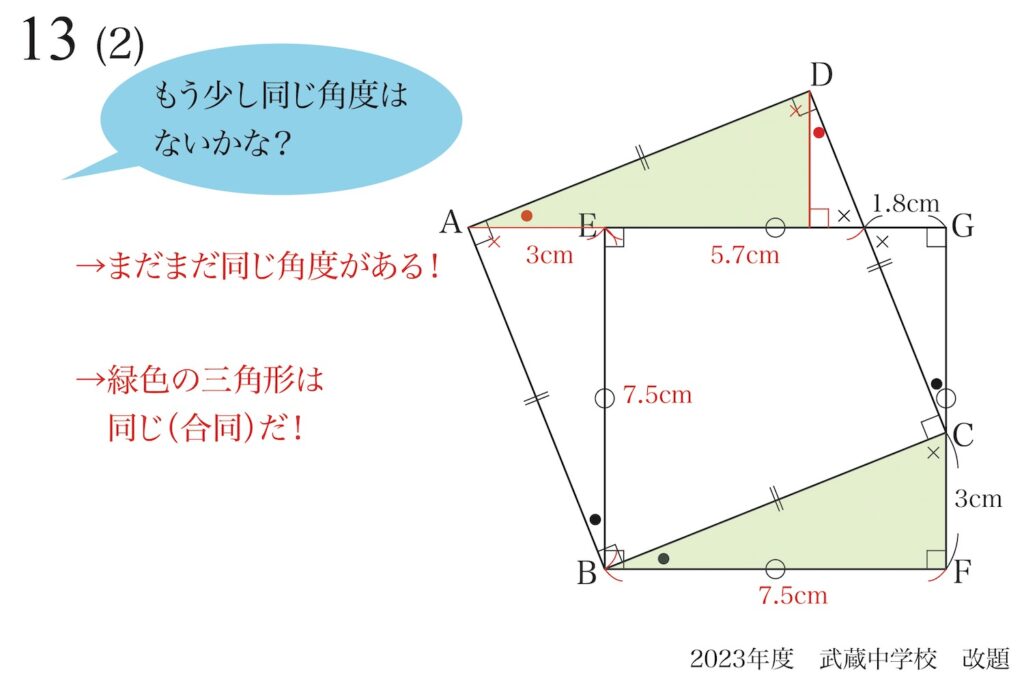
合同図形を見つける話を、上記リンクでご紹介しています。
女子小学生この考え方だと、
合同な図形が大事だね・・・
「図形問題は相似形」と言っても良いほど、「相似比が決定的に重要」である図形問題。
その一方で、時々「合同図形が登場する」ことがあります。
女子小学生相似形と合同図形と
どっちを考えたら良いのかな？
女子小学生やっぱり、
相似形のほうが多いから・・・
女子小学生合同図形は、
あまり考えなくても良いのかな・・・
相似形では比が大事ですが、合同図形は「同じ」です。
・合同図形は「「相似比1:1」の相似形
・図形問題は同じ角度を探して、相似形を探す
合同図形は「「相似比1:1」の特殊な相似形です。
この視点から考えると、合同図形を探すのは「相似形を探す」ことと同じことになります。
25Speed117ts
「比を考える」発想の観点から考えると、図形問題と速さなどの比の問題は似ている面があります。
算数を学ぶ際には、旅人算・ニュートン算・和差算・図形・・・など各単元で学ぶことが多いです。
中学受験の場合、小学6年生の10月頃〜直前期は、「複合的に考える」視点を持つと良いです。
すると、応用問題を解く力がアップするでしょう。
次回は上記リンクです。
