前回は「算数の学力を大幅アップする学び〜「比の問題」と図形問題の類似・速さ・比の出題が多い理由・作成しやすい「様々なシーン」〜」の話でした。
「視点を変えて」算数の問題を解くコツ：
25Speed205ts
算数実践問２０の問題は、「視点を変えて」考える点が最も重要でした。
出題者Aに追いついてから
Bに追いつくまでの時間は・・・
出題者午後2時からAに追いつくまでの時間の
6倍の時間がかかりました。
出題者は、Cが追いつく時間として「1:6」という比を提示しました。
普通に問題を解く考え方であれば、この「1:6をそのまま使う」発想になります。
25Speed208ts
ここで、「1:6」という関係に対して、「「1:(1+6)=1:7」と考える点がポイントでした。
この問題を解く話を、上記リンクでご紹介しています。
男子小学生この考え方は、
説明されれば、なるほどって思うけど・・・
女子小学生「比を足して考える」は、
テストで思いつかないかも・・・
このような「視点を変える」発想は、算数・数学では非常に重要です。
「ほんの少し見方を変える」ことで、すっきり見えてくることがあるのが算数や数学です。
男子小学生「ほんの少し見方を変える」ことが
もっと出来るようになりたい・・・
今回は、この「「ほんの少し見方を変える」力を増強するには、どうしたら良いか、の話です。
「ブロックの見方」を復習：「前から」「右から」「斜め上」から見る視点
算数を学び始めて、しばらく時間が経つと、上のように「ブロックの問題」が登場します。
女子小学生この問題は、
一時期、結構やったね！
入試本番でも登場することがある、この「ブロックや積み木の問題」。
これらのブロックの「面の数」などが問題になることがあります。
ブロックの数が多くなると、考えるのが難しくなり、難問になります。
ブロックを考えて「分かるようになる」話を、上記リンクでご紹介しています。
この「ブロック・積み木の問題」は、「ある面を正面から見る」視点が大事です。
出題者このブロックの表面積は
〜cm2でした・・・
出題者このブロックの体積を
答えてください。
このように、多数のブロックの表面積と体積の問題も多くあります。
ここで、たくさんあるブロックの表面積を考える際には、様々な視点から見た図が有効です。
あるいは、「一つの面には６面あり、ブロック同士がつながると双方で面が２減少する」と考えるのも良いです。
いずれにしても、ブロックの問題では、「立面図=ある面をまっすぐ見て考える」ことが多いです。
その一方で、上のように「斜め上から見る」のも大事です。
「斜めから見る」視点は、算数の問題を「解く鍵」になるかは問題によりますが、全体像がよく分かります。
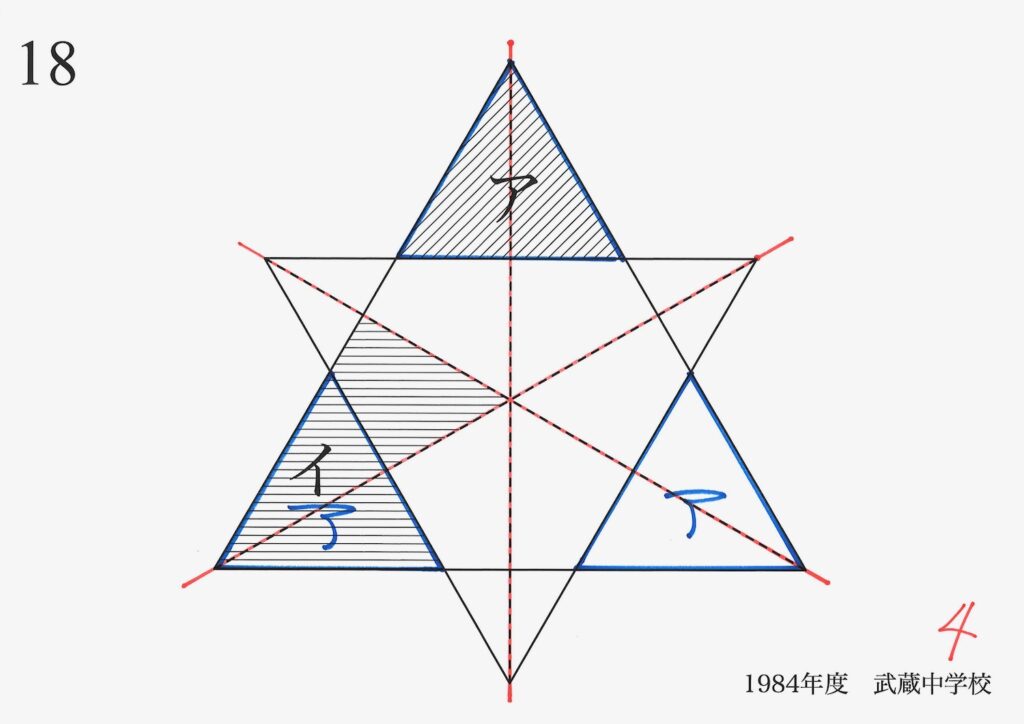
問題文の文章が短めであれば、比較的全体像を理解するのは簡単です。
上の図のように、「正三角形が二つ」の図形問題は、状況を理解するのは比較的簡単です。
上の問題の解き方を、上記リンクでご紹介しています。
食塩水の問題では、「一部を取り出して混ぜて、さらに取り出して・・・」という問題があります。
この問題の状況は、冷静に考えると分かりますが、色々と混ぜているうちに、
男子小学生あれ？
結局、どうなるんだっけ？
状況が分からなくなって、混乱してしまうことがあります。
「状況が適切に把握できない」場合、算数の問題が解けることは、ほとんどありません。
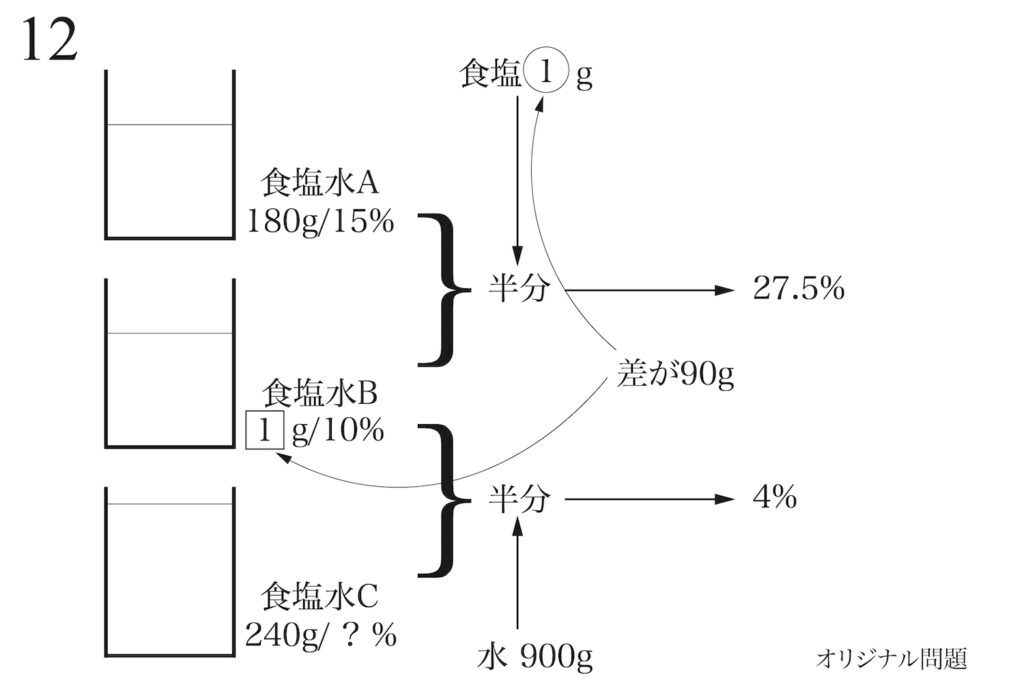
このように、食塩水A,B,Cなど登場して複雑な場合は、図に描いて整理する姿勢が大事です。
そして、「どのような視点、切り口で考えると解けるか」を考えると良いでしょう。
・問題の状況や内容を整理して図を描く
・解く視点や切り口を考える
この「全体像を見る考え方」によって、問題を多角的に考えることが出来るようになります。
算数の応用問題・難問を解く際には、「どこに注目するか」が分からないと進まないことが多いですが、
女子小学生ここをこのように
考えたら・・・
女子小学生あっ、これって
こういうことかな・・・
「解く視点や切り口」を考えると、解けることが多いです。
そして、「解く視点や切り口」こそが、算数の難問・応用問題を解く時に最も重要です。
様々な解法が身についた直前期は、「多角的視点」を考えるようにすると応用力がアップするでしょう。
算数の「多角的視点」は、ブロックの見方を復習するのも良いと考えます。
