前回は「電気・電流のわかりやすい考え方・コツ 2〜電流を持ち上げる高さ=矢印の数・直列と並列・理由を理解して暗記・直列つなぎのイメージ・便利な矢印〜」の話でした。
電流の流れと電池の役割:〜ボルトの電池
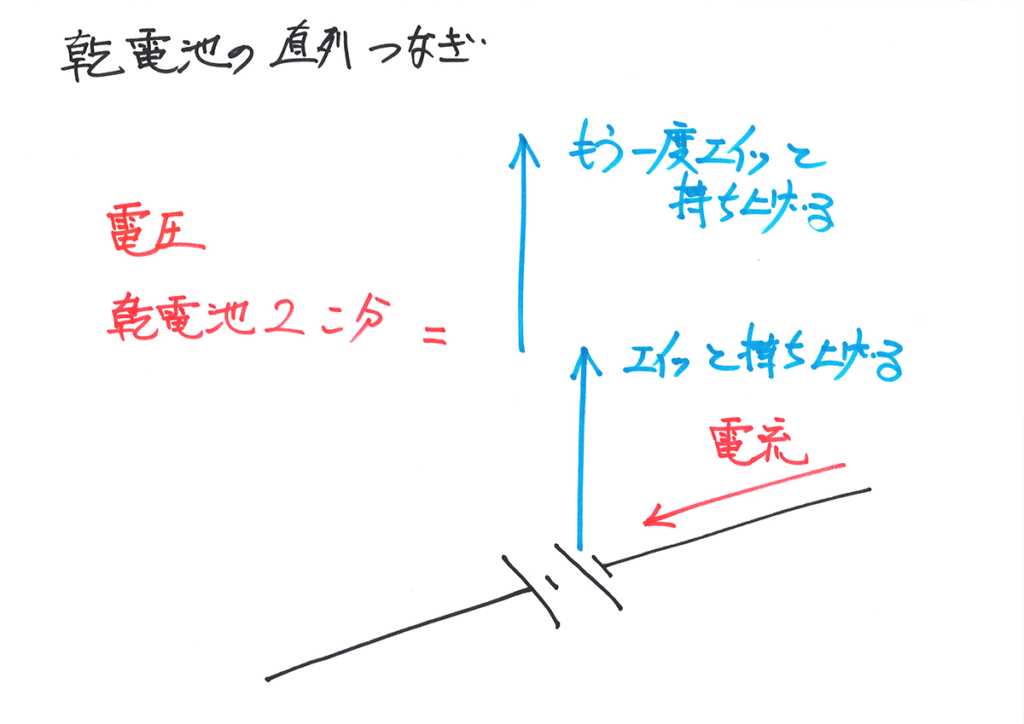
電池は「電流をエイッと持ち上げる」役目をするイメージを持ちましょう。
電池を持ち上げる向きは、「基本的に上」です。
 電池
電池電流を上に
持ち上げるよ!
その時に、電流を持ち上げる高さを矢印で表現すると分かりやすいです。
・矢印の長さ:電流を持ち上げる高さ(起電力)
この時、持ち上げる高さを「〜ボルト」と表現します。



単三乾電池は
「1.5ボルト」とかって言うね!
この「〜ボルト」が「持ち上げる高さ」の大きさ・長さになります。
基本的には、「電圧=持ち上げる高さ=矢印の長さ」は全部共通です。
問題によっては、「持ち上げる高さ=電圧」が異なる電池が出るかもしれません。
この「持ち上げる高さ=電圧」などを変えるために、「直列・並列」が登場します。
矢印を考えたら、「N個の直列=N個分の高さ(電圧)が上がる」ことが分かりました。
そのため、1.5ボルトの電池を10個直列につないだ場合は、どうなるか考えてみましょう。



1.5×10=15ボルトの
持ち上げる高さ=電圧!



そう考えると、
電池の役割がよく分かるね・・・
このように、「電池の直列は〜」と丸暗記しても良いですが、意味や役割を知ると楽しくなるでしょう。
そして、その「理科への楽しさ」は成績アップにつながるでしょう。
電池の並列つなぎ
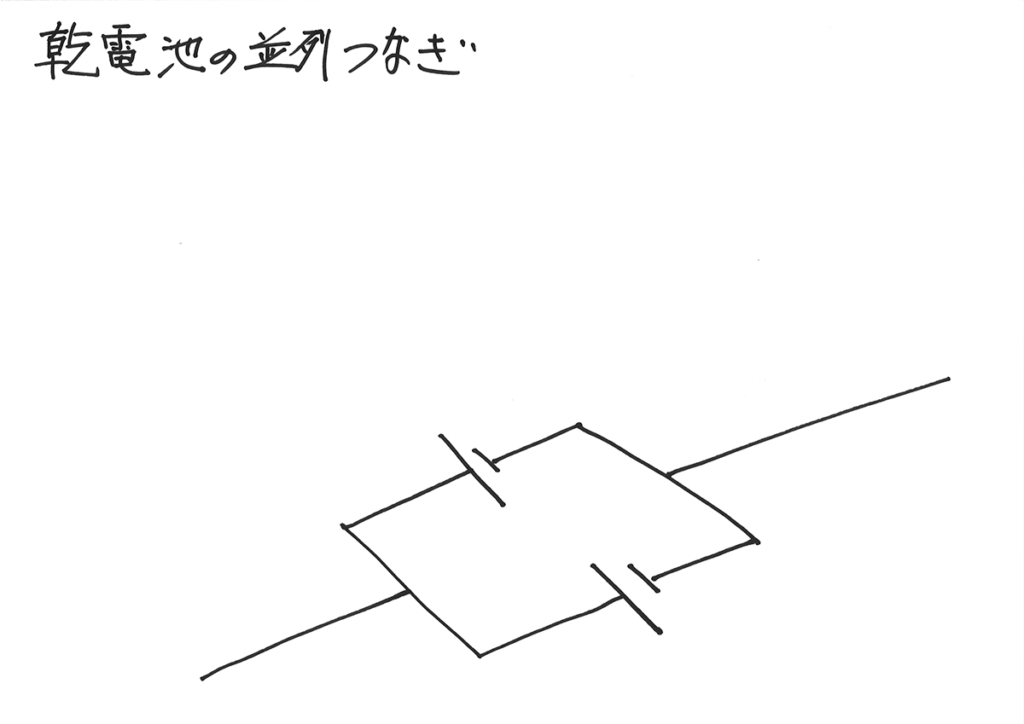

今回は、並列電池を考えましょう。
直列電池の時と同じように、流れる電流を描きましょう。
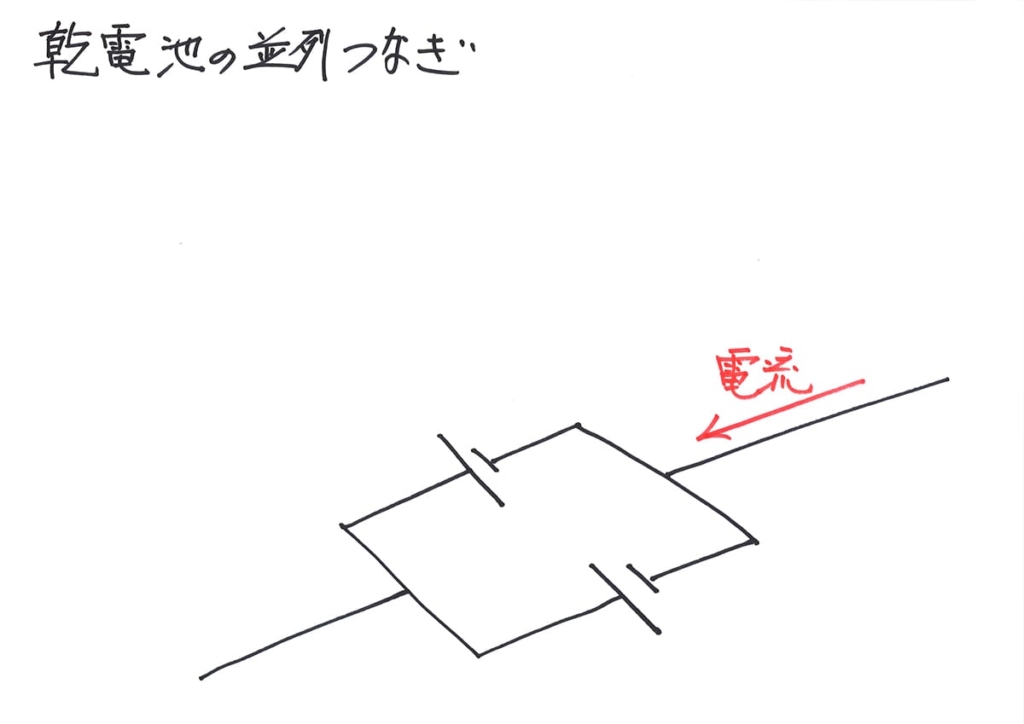

電流が流れてきて、並列電池のところにやってきます。



回路を
流れてきたよ!



あれ?回路の線が
二つに分かれているね・・・
すると、線が分かれているので、



じゃ、僕(電流)も
二手に別れようか!
電流も分かれます。
直列の時と同じで、「まずは、電池がエイッと電流を流す」と考えましょう。
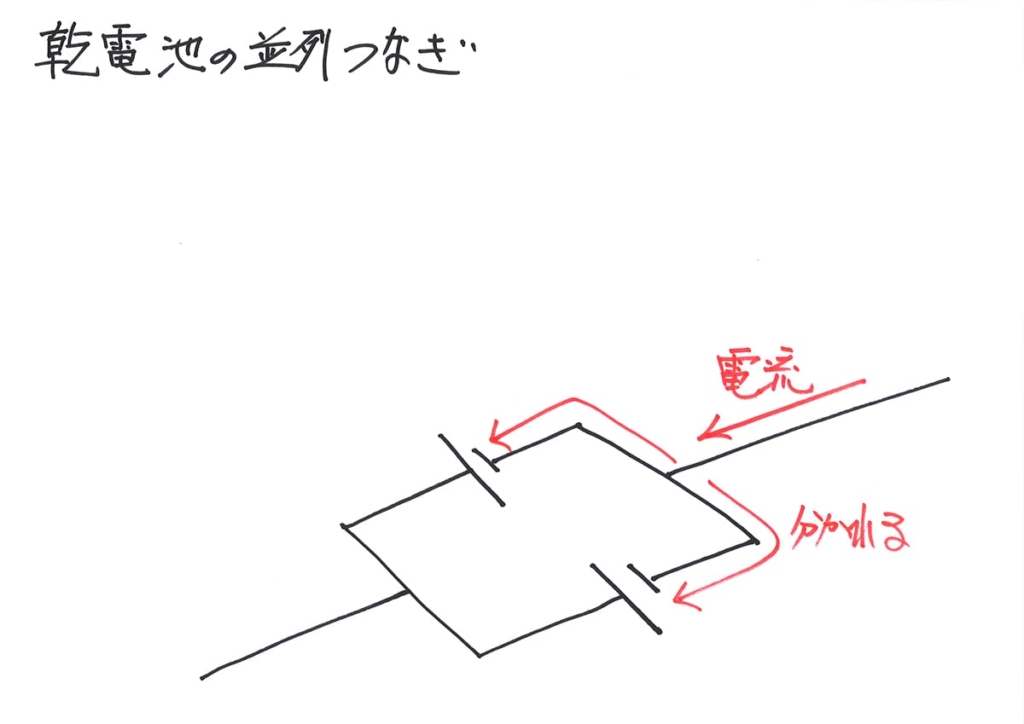

同じように電池が「電流を持ち上げる高さ」を矢印で描いてみましょう。
それぞれの電流が、それぞれの電池によって、エイッと持ち上げられます。



僕(電池)が電流を
持ち上げてあげるよ!
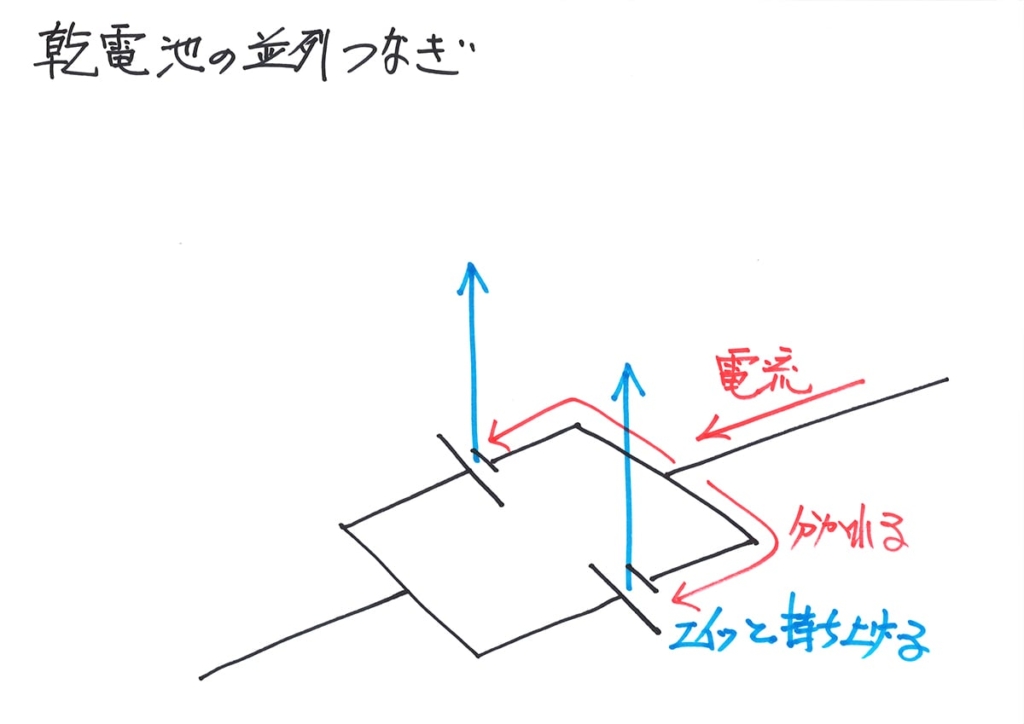

電池に持ち上げられた電流は、また流れることが出来るようになります。



電池さん、持ち上げて
くれて有難う!



また来たら、
持ち上げてあげるよ!
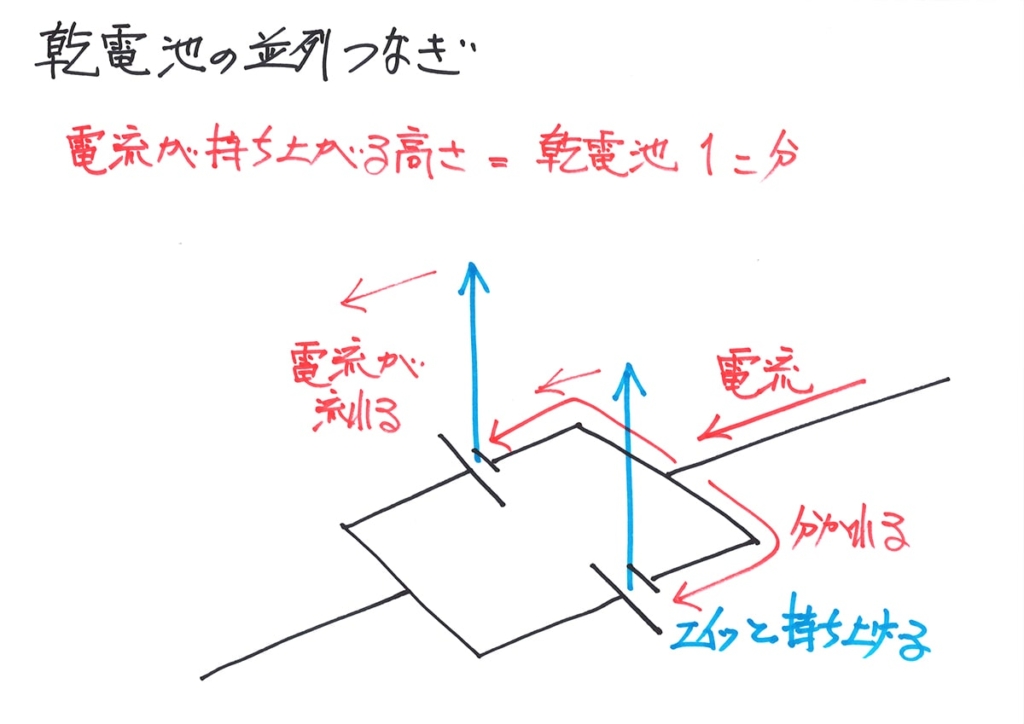

電流が持ち上がる高さを、水色の矢印で描きました。
直列の時と大きく違うのは、「それぞれの電流が電池一個分(矢印一つ分)持ち上げられる」ことです。
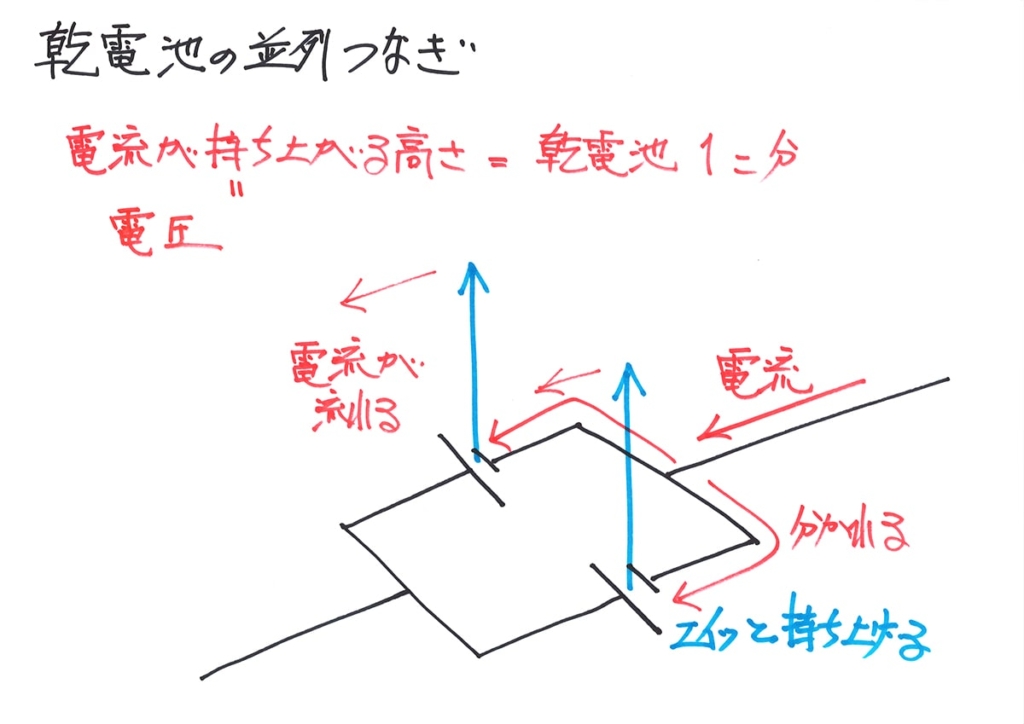

そして、この場合は、「矢印一つ分=電池一つ分が電圧」になります。
これで、「並列電池は電圧は電池一つ分」が分かりました。
・電流は、「電池1個分の高さ=電圧」持ち上げられる
回路の対称性:算数と理科の似ているところ
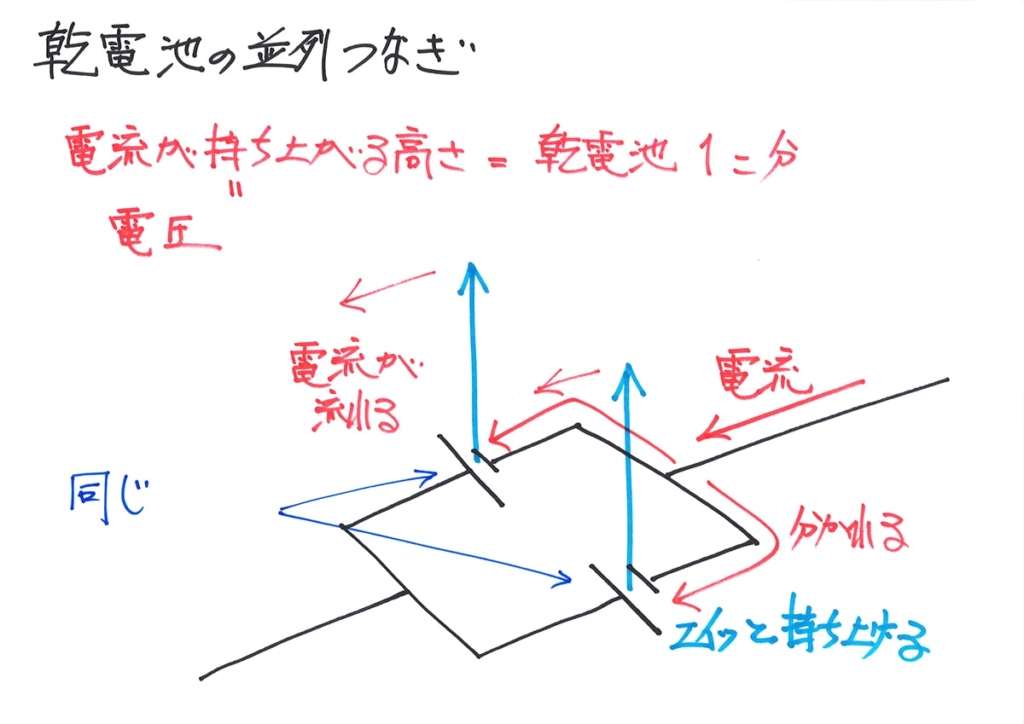




これで「電池の並列つなぎ」が
「電池一個分の電圧」が分かった!



私もちゃんと
説明できそう!
もう少し考えてみましょう。
並列電池のところで、電流が分かれましたが、分かれた先が同じ(対称)です。



分かれる先の
回路が同じだから・・・



僕も二手に分かれて、
ちょうど半分ずつになろう・・・
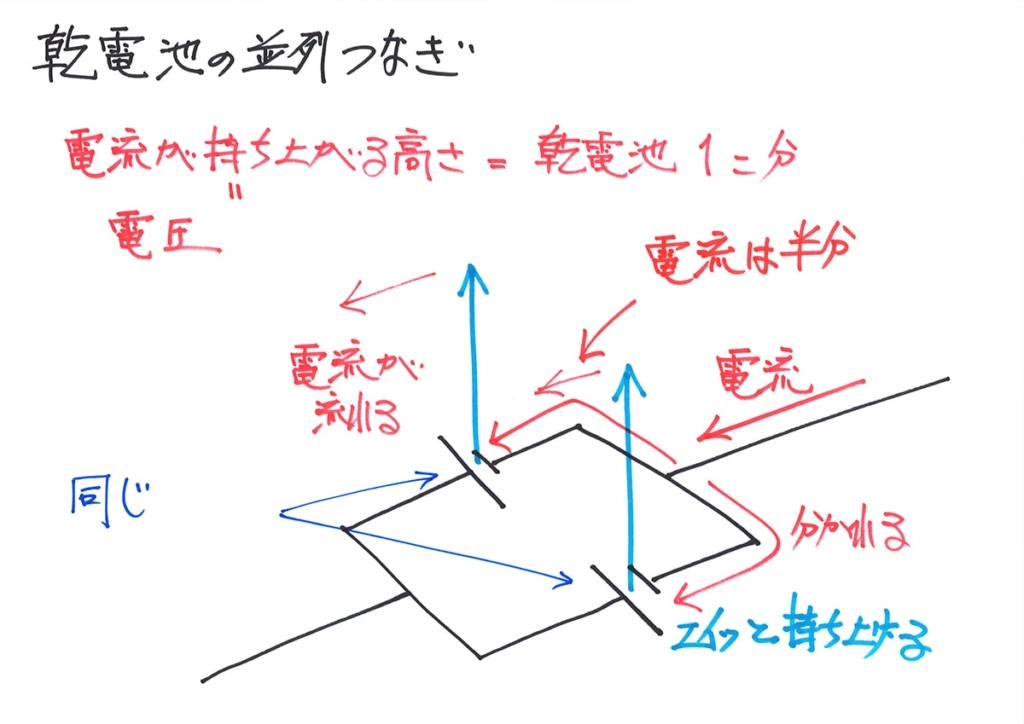

「同じ」なので、分かれる電流は半分になります。
すると、電池にゆく電流は半分になります。
電流を持ち上げる電池にとっては、電流が半分だと「持ち上げるのが楽」です。



電流さんが
半分になったから・・・



持ち上げるのが
半分で済むから楽だね!
荷物を運ぶときのことをイメージしてみましょう。



荷物は軽い方が
持ち上げやすいね!
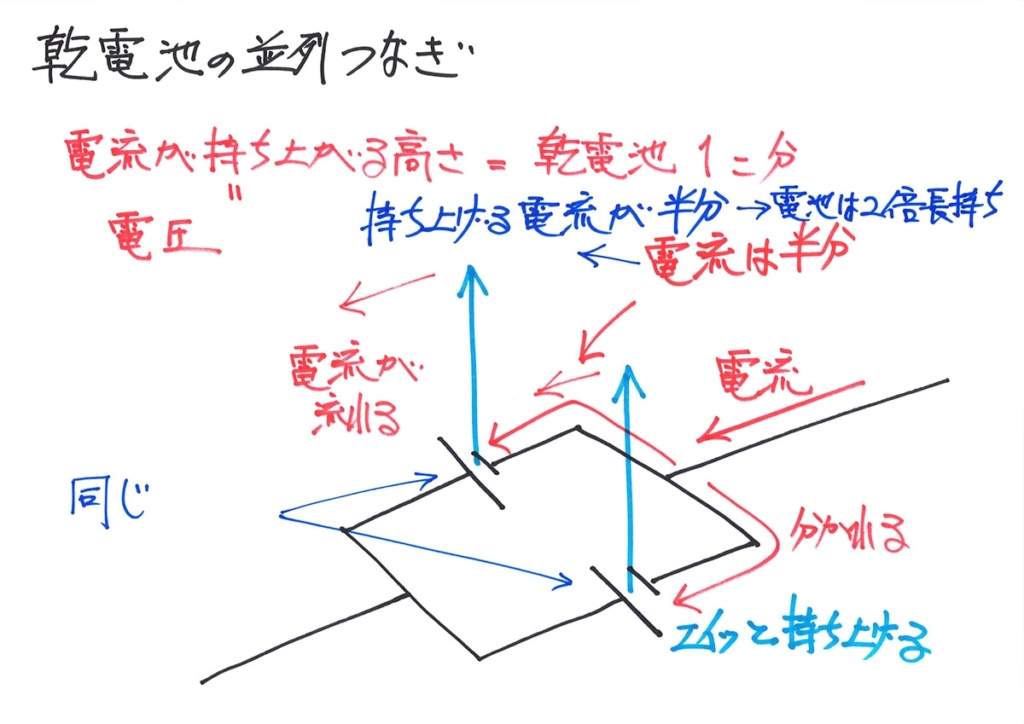

持ち上げる電流が1/2になって、電池が楽になるので、電池は2倍長持ちします。
これで、電池の直列つなぎ・並列つなぎで、もう一つ大事な性質が出てきました。
・電流は、「電池の個数分の高さ=電圧」持ち上げられる
・電池の「持ち」は変わらない(流れる電流が同じ)
・電流は、「電池1個分の高さ=電圧」持ち上げられる
・電池の「持ち」は、並列電池の個数分長くなる(流れる電流が減少する)
直列・並列ともに、それぞれ特徴があります。



こうして電流を描いて、
電池の矢印描くと、分かりやすいね。



直列も並列も
しっかり理解できた!
応用問題も「基本の積み重ね」です。
算数・理科は、「基本をしっかり」すれば応用問題も出来るようになります。
応用問題は、「基本を積み重ねたり、組み合わせる」考え方でやってみましょう。



今まで、電流を描かないで、
直列・並列を公式に当てはめていた・・・



こうして、電流の流れを考えると、
イメージしやすい!
ぜひ、電流の流れ・電池の矢印を描いて、イメージしてみましょう。
また、今回「対称性」の話をしました。



対称性は、
算数の図形だけだと思っていたよ・・・



理科で
出てくるとは思わなかった・・・
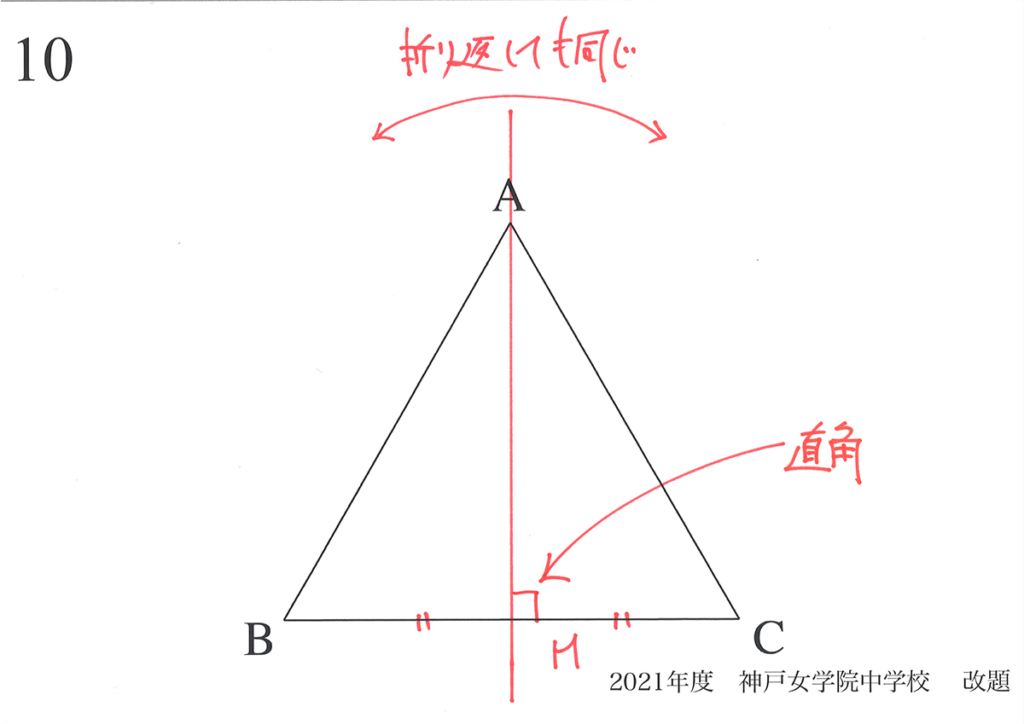

正三角形には、対象となる線(軸)が三本あります。
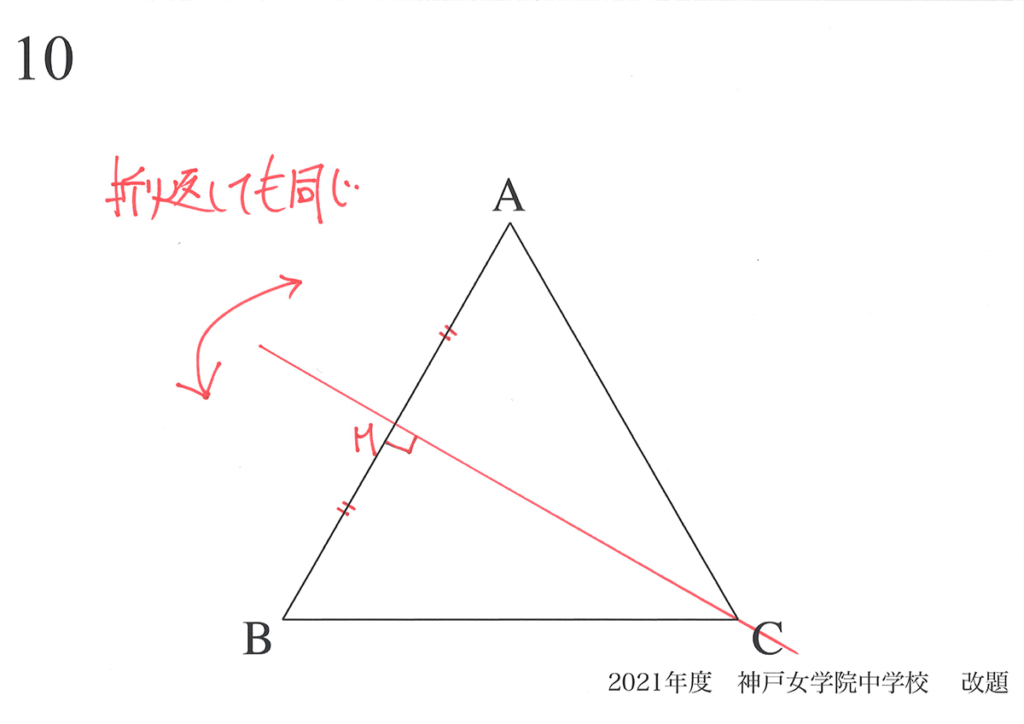

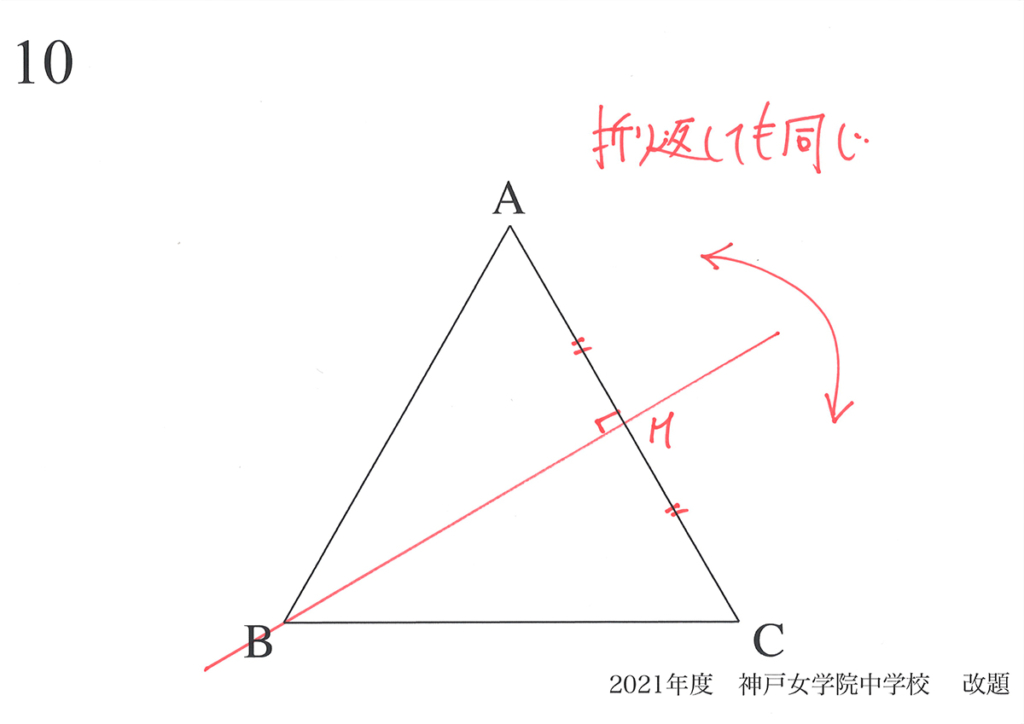

三角形の対称性に関する話を、上記リンクでご紹介しています。
対称性は図形だけではなく、様々なところにも出てきます。
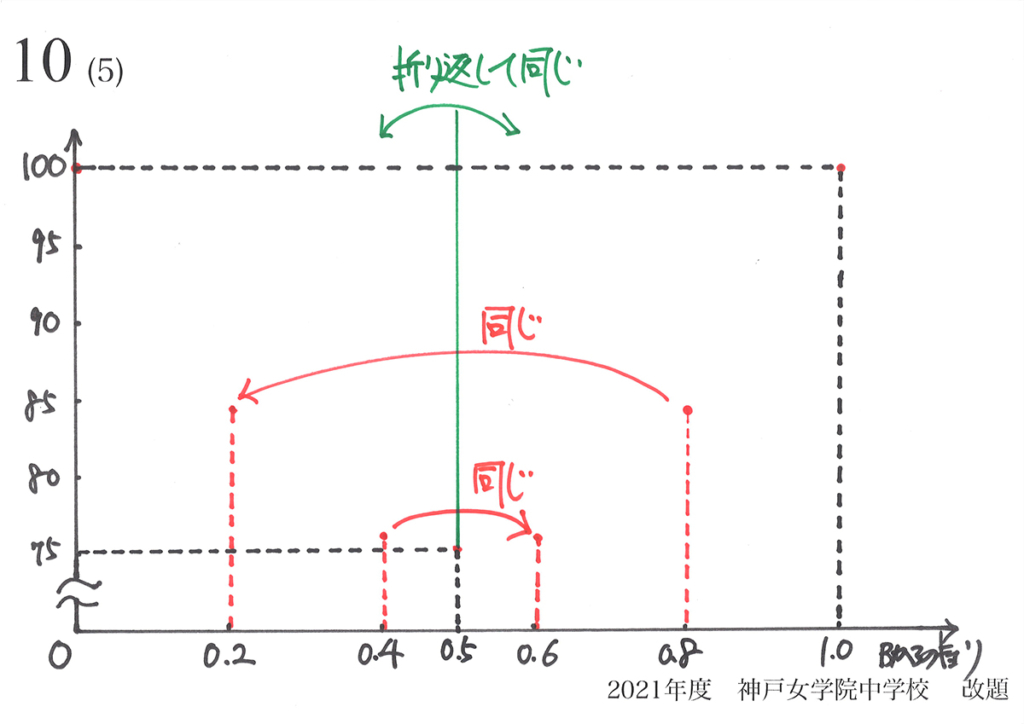

「正三角形の対称性」から「グラフの対称性」の話をご紹介しました。
このように「折り返しても同じ」という対称性の性質は、算数・理科では非常に大事です。



対称性って
見つけたら、楽しそう・・・
中学受験では少ないかもしれませんが、数式などでも「対称性」が大事な場合もあります。
このように、算数と理科を横断的に見る視点は楽しく、発展的です。
こういう考え方も知りながら、楽しく学力アップしてゆきましょう。
次回は抵抗の話で、下記リンクです。




