前回は「地球の自転と公転のなぜを理解する考え方〜公式を導出できる学び・地球が太陽の周りを常に周っているイメージ・夏至と冬至と春秋分の具体的イメージ・夏至は暑くて冬至は寒い・猛烈な太陽のイメージ・万物の恵みと核融合〜」の話でした。
問題5:地球の自転と公転


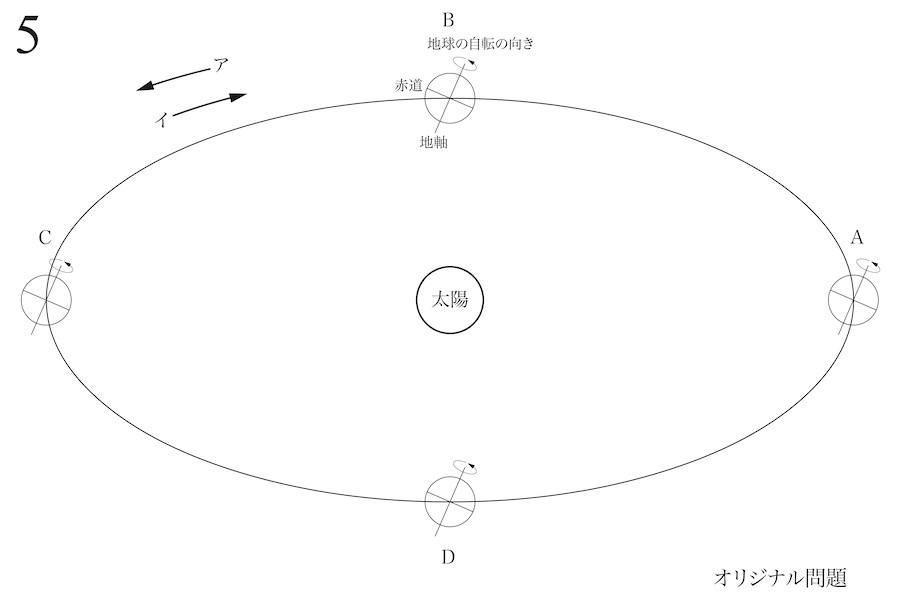
地球は太陽の周りを1年で1周し、この運動を地球の公転と呼びます。
地球は公転面に対して少し傾いていて、地球の中心を通る自転軸を地軸と呼び、公転面に垂直な方向から23.4度傾いています。
以下の問いに答えなさい。途中経過の式なども書きなさい。
(1)地球の公転の向きは、図のア、イのどちらか、記号で答えて下さい。
(2)地球の地軸が公転面に垂直な方向から傾いていない時、どのようなことが起こるか、答えて下さい。
(3)実際に地球の地軸が公転面に対して傾いている事が、私たちの日常生活にどのように影響してますか。あなたの意見も含めて、答えて下さい。
(4)地球の位置が太陽に対して、A,B,C,Dの位置にある時、それぞれ下記のどの時期に当たるか。記号で答えて下さい。
選択肢:春分、夏至、秋分、冬至
(5)A,B,C,Dの中で、地球の全ての地点で昼の時間と夜の時間の長さが同じになるのは、どの点ですか。
理由も簡潔に答えて下さい。
3DCGで太陽の光をイメージ:昼と夜の長さ
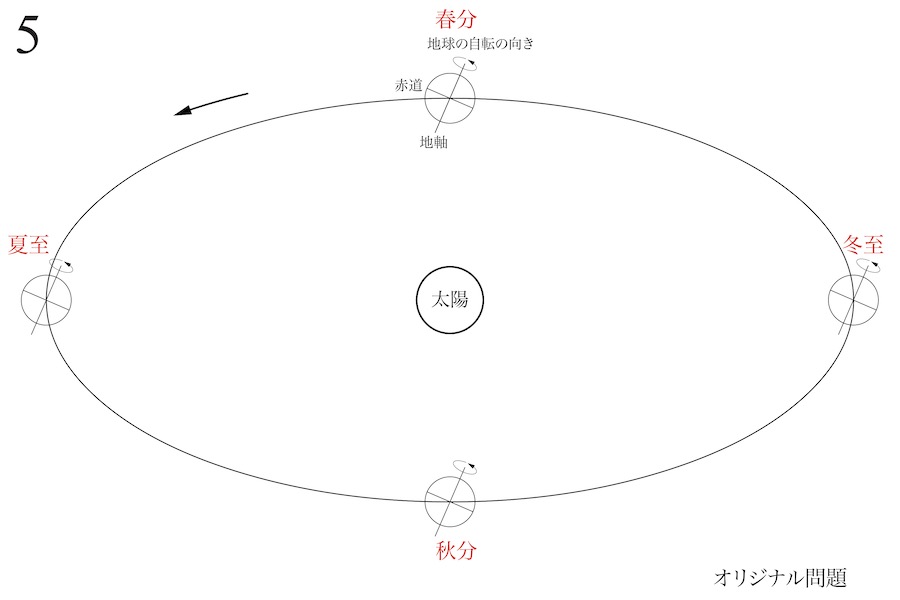
太陽と地球の位置関係を考えて、春分・夏至・秋分・冬至を考えました。
・夏至は真夏で暑い
・冬至は真冬で寒い
・春分と秋分は、夏至と冬至の間の雰囲気
この問題は、暗記していて「即答できた」方もいるでしょう。
「答えだけ」でも記述タイプのテストでも、「理由を理解している」と理科は解けるようになります。
この意味では、(5)も暗記で「答えを分かっている」方が多いでしょう。
 男子小学生
男子小学生これは、
春分と秋分だよ!



私も分かるけど、
理由を説明するのは、難しいかも・・・
天体の問題に限らず、「知っていること」の理由を説明することは意外と難しい面があります。
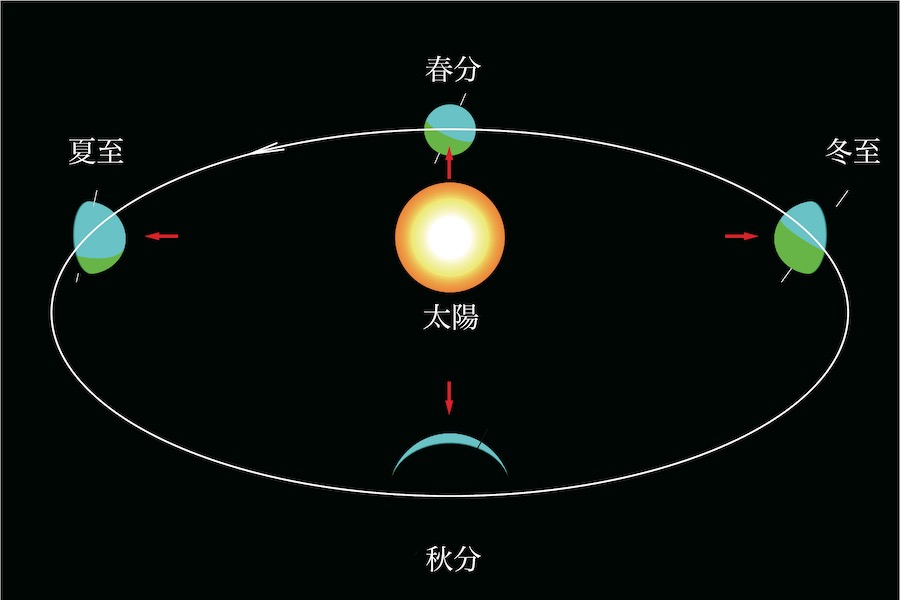
上の図は「3次元を2次元で描いた」図ですが、今回は3DCGの図を見ながら考えてみましょう。
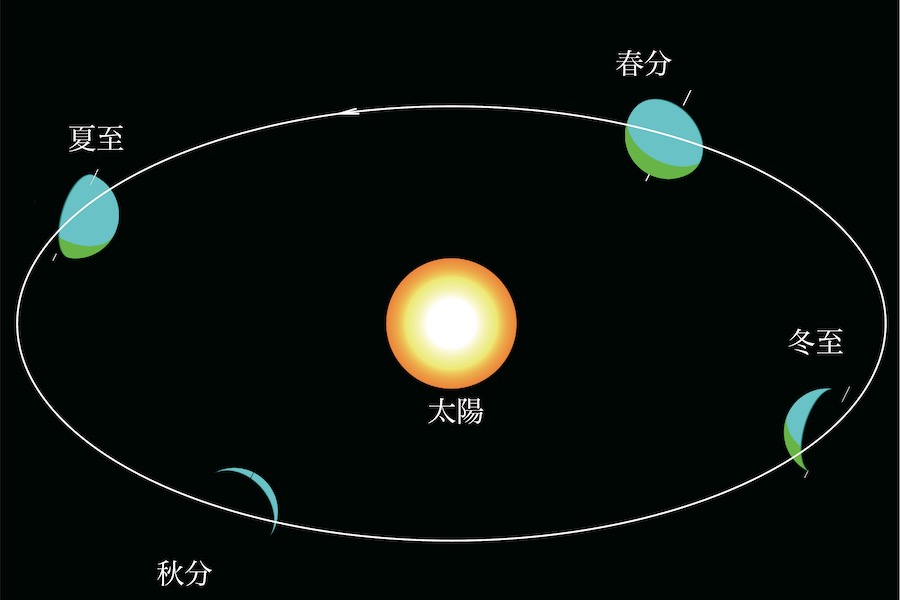

上の「地球と太陽」の図を斜め上から見た図です。
公転面などを描いており、「太陽から太陽光線が放たれている」状況です。
北半球を水色・南半球を緑色で表現しています。
これらの状況を拡大して、夏至→冬至→春分→秋分の順番で見てみましょう。
公転を考えると、春分→夏至→秋分→冬至の順序が筋かもしれません。
このように「何かの性質・状況」を考えるときは、最も極端な状況を先に考えるのが良いでしょう。
・夏至は真夏で暑い
・冬至は真冬で寒い
・春分と秋分は、夏至と冬至の間の雰囲気
すると、夏至か冬至かが最も極端なので、夏至を考えます。
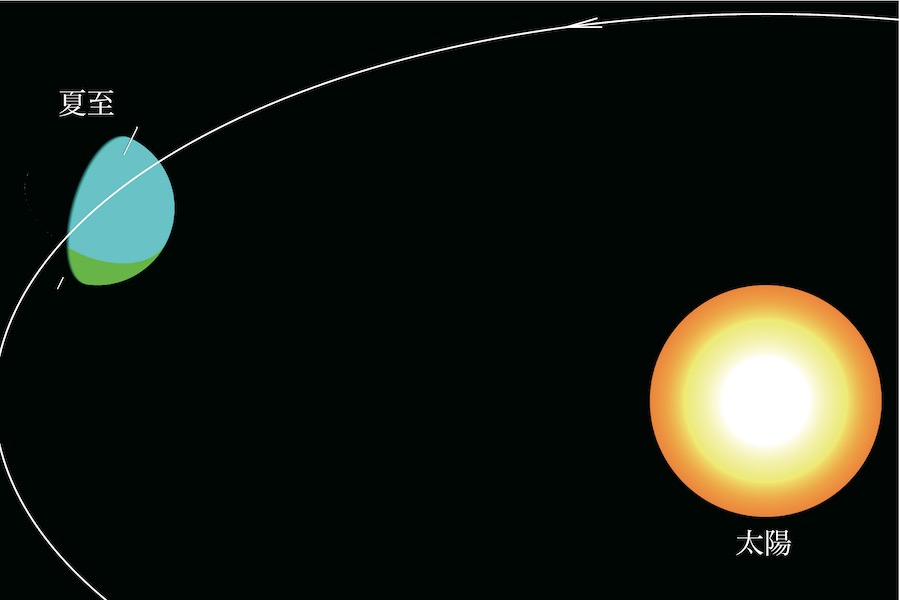

まずは、北半球に最も太陽光が当たる夏至を見てみましょう。
夏至の時に、北半球が太陽から太陽光線をたくさん浴びている状況が分かります。
・自分が住んでいる北半球(南半球)を優先して状況を理解して、その後逆を考える
・南半球で起こることは、北半球の逆(北半球で起こることは、南半球の逆)
そのため、北半球では昼の長さが長くなり、南半球では逆の夜の長さが長くなります。
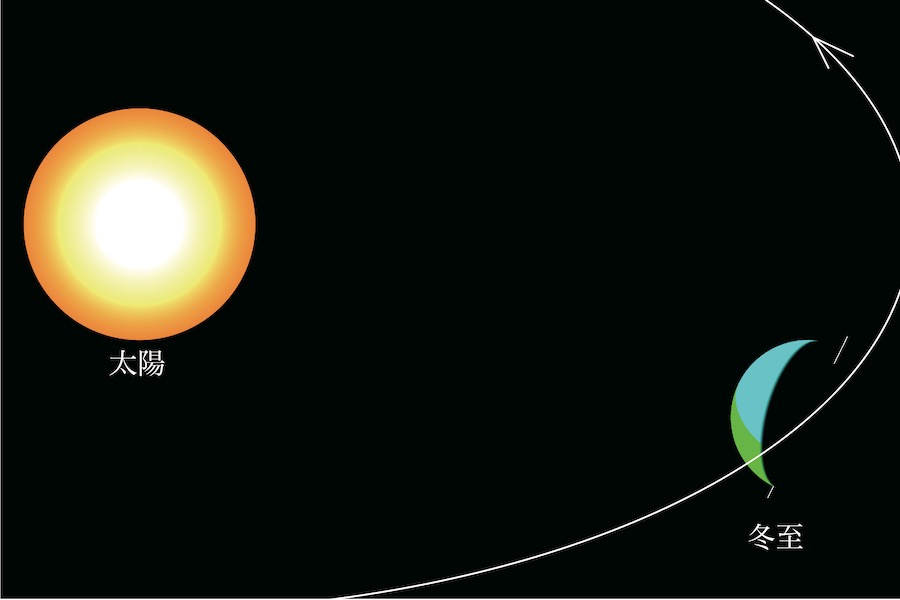

反対に、冬至は北半球に当たる太陽の光が少ない状況が分かります。



これは
分かりやすいね!



だけど、見る角度によって
光が当たる面が少し変わるのでは?
後ほど、太陽から見た向きのCGをお見せしますが、まずは「斜め上から」の絵で比較しましょう。
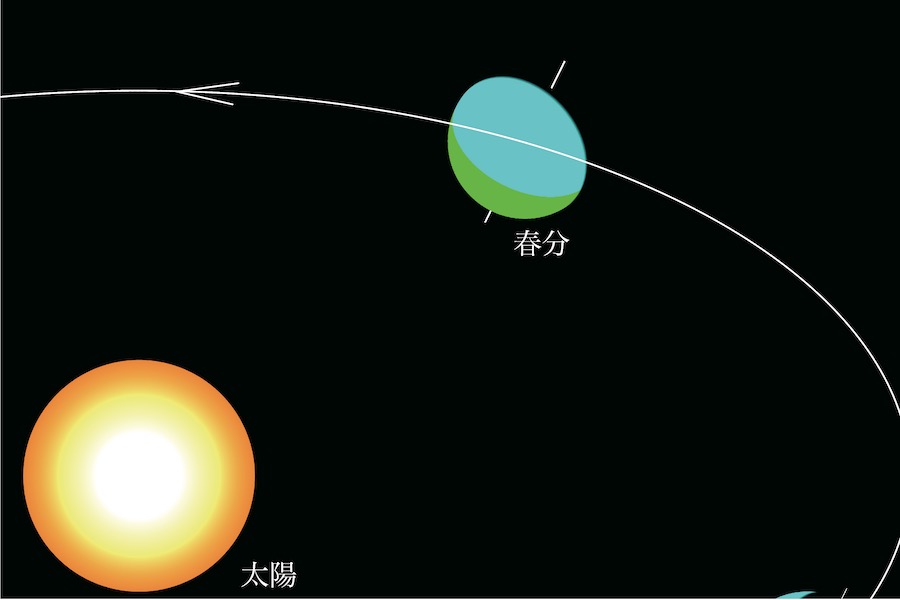

春分は、太陽の光が満遍なく当たっている感じです。
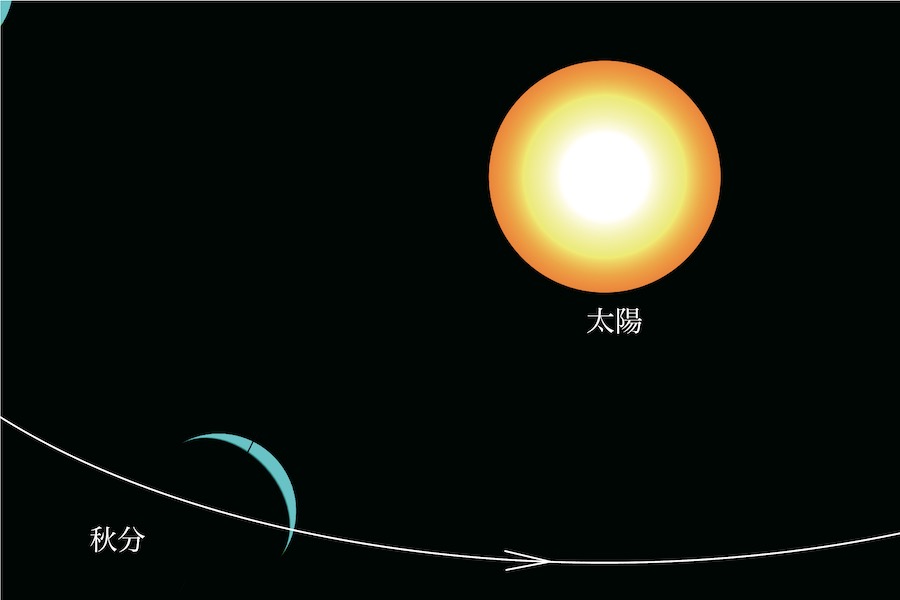

秋分の状況は、この「斜め上」からの視線では「後ろ側」になってしまうので少し分かりづらいです。
異なる角度から地球と太陽を見るイメージ:地軸の向きと太陽光
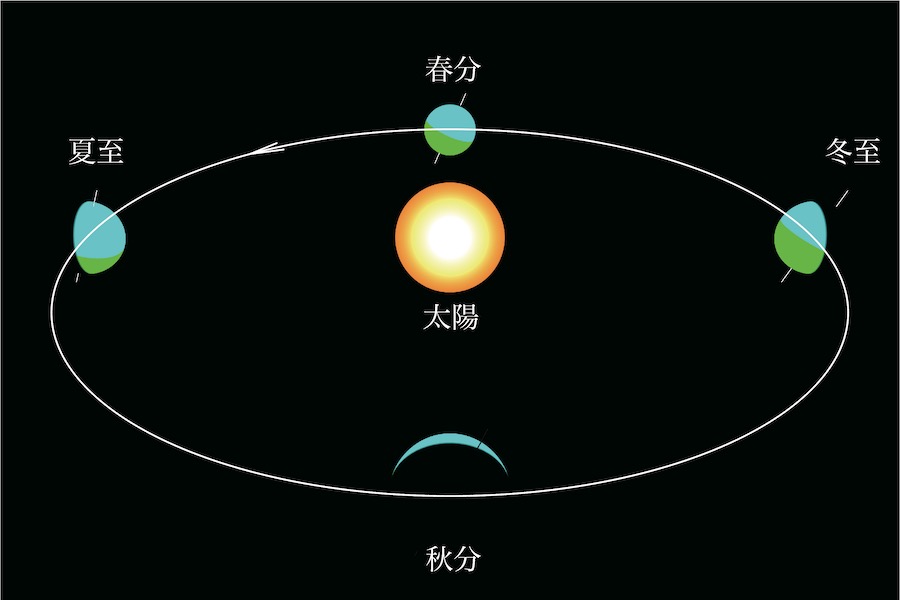

今度は、見る視線を変えてみましょう。


最初の2次元平面の図で、「秋分の方に立って、少し上から眺めた」図です。



この図も面白そうだけど、
秋分が分かりずらいかな・・・

そこで、それぞれ「太陽側から見た」CGを見てみましょう。
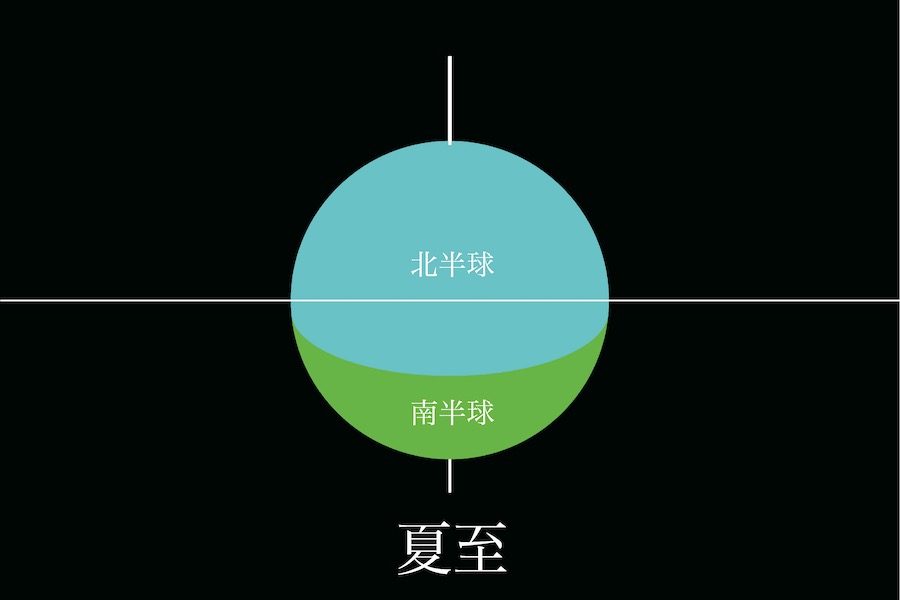

夏至は「北半球に大量の太陽光が降り注いでいる」のが分かります。
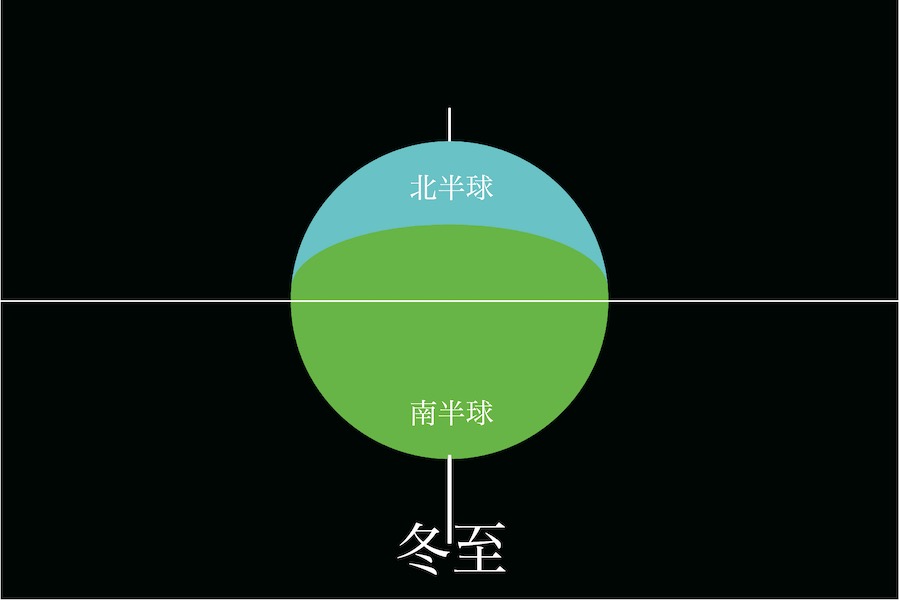

冬至は「夏至と地軸の向きが逆」であることをイメージしましょう。
すると、「北半球が向こう側」になっていて「南半球に大量の太陽光が降り注いでいる」のが分かります。
人の姿勢に例えると、「北半球が頭で南半球が足かお尻」のイメージでも理解しやすいでしょう。
「姿勢が逆」になっているので、「光の当たり方も逆」になります。
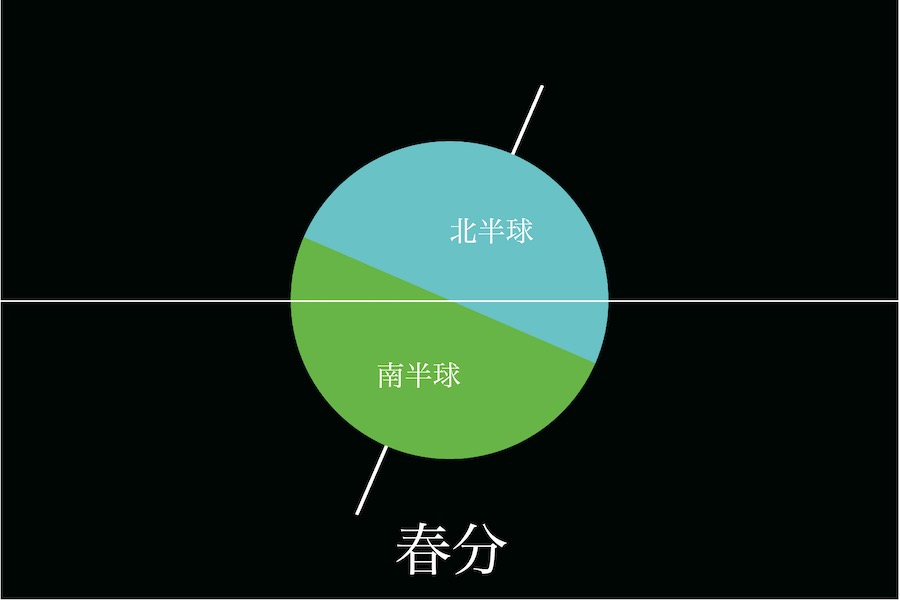

春分は「太陽側から見て地軸がやや右に傾いて」いて、北半球と南半球に等しく太陽光線が当たっています。
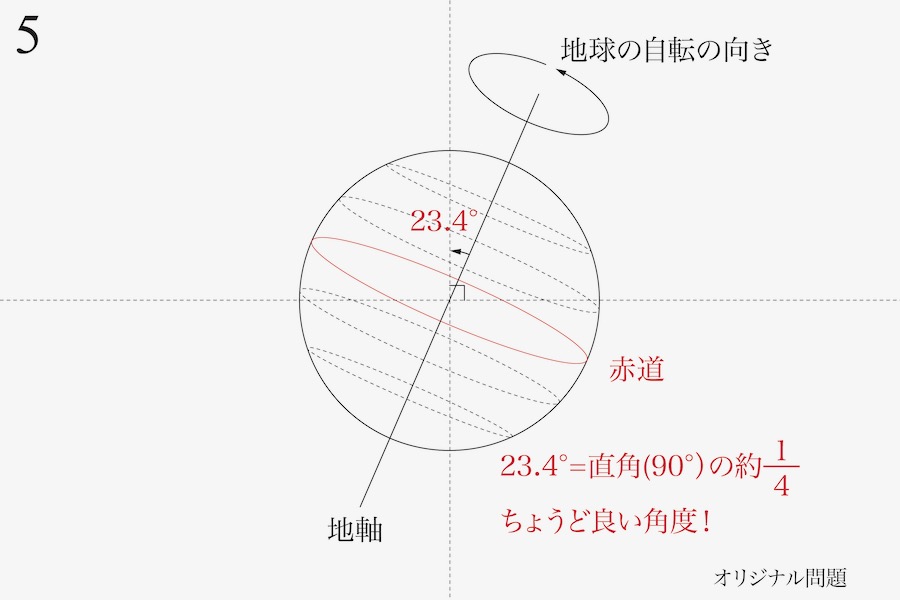

地球のみを拡大した図は、この「春分の時に太陽から見た図」になります。
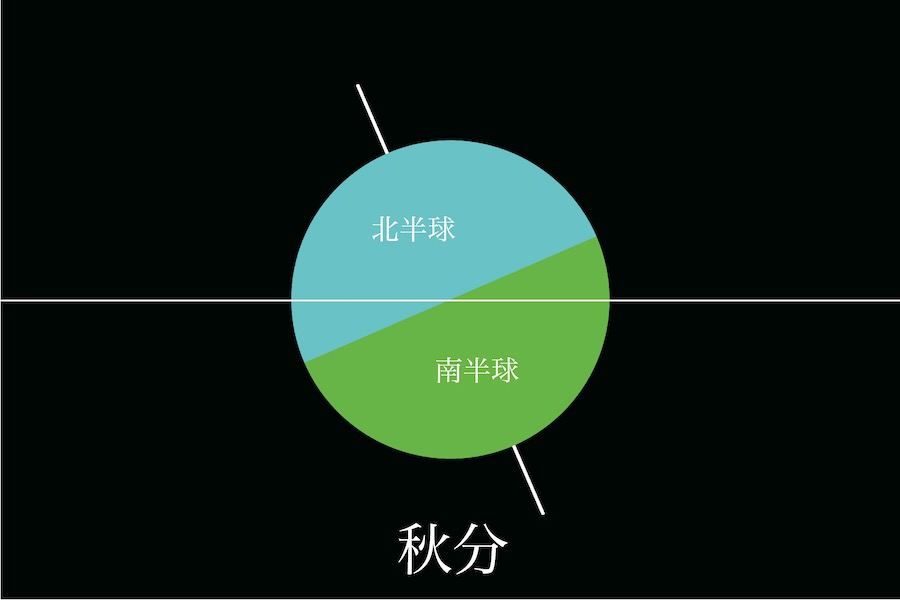

秋分は「太陽から見る」と、「春分のちょうど左右反対」になります。
ここで、「太陽側から見て地軸がやや左に傾いて」いる」事実が大事です。
秋分は、北半球と南半球に等しく太陽光線が当たっています。



確かに、こうして見てみると、
違いがよく分かる!
2次元の平面で考えて、地球に太陽光線を当てた絵を描いて理解できると良いでしょう。
ただ、2次元で考えていると、地球や太陽が「円である」ように誤解して考えてしまう可能性があります。



確かに、平面で描いていると
円だと思っちゃう時ある・・・
円と球は似ている面がありますが、2次元と3次元では全く違います。
算数の立体問題を考えるときに、「ある面で切断して考えて、3次元を2次元にする」ことがあります。
それは「2次元の方が3次元よりも、はるかに分かりやすい」からです。
この地球の自転と公転は、できれば「3次元をイメージして、2次元で描いて考える」と良いでしょう。
・BとD(春分と秋分)
・理由(解答例)
a.太陽光の光の向きに対して、地球の北半球と南半球が等しくなり、地球上の全ての場所(地点)で同じように太陽光が降り注ぐから。
b.太陽光の向きに対して垂直な面を考えると、ちょうど地球の北半球と南半球の面積が等しくなり、地球上の全ての場所(地点)で太陽光が照らす時間が同じになるから。
新たな要素を付加:自分なりに理解する姿勢


この春分と秋分は「北半球と南半球が、太陽に対して完全に等しい面になる」事実。
2次元だと分かりにくいのが、3次元だと分かりやすいと思います。
それでも、



ちょっとピンと
来ないんだけど・・・



僕って、理科のセンスが
ないのかな・・・
このように悩む方もいるかもしれません。
こういうことを「パッと分かる」かどうかは、センスとはあまり関係ないでしょう。
そもそも、「分かっている」方も「どの程度分かっているか」は不透明な面があります。
そのため、「ピンとこない」時は、描いたりして「自分なりに理解する」のが良いでしょう。
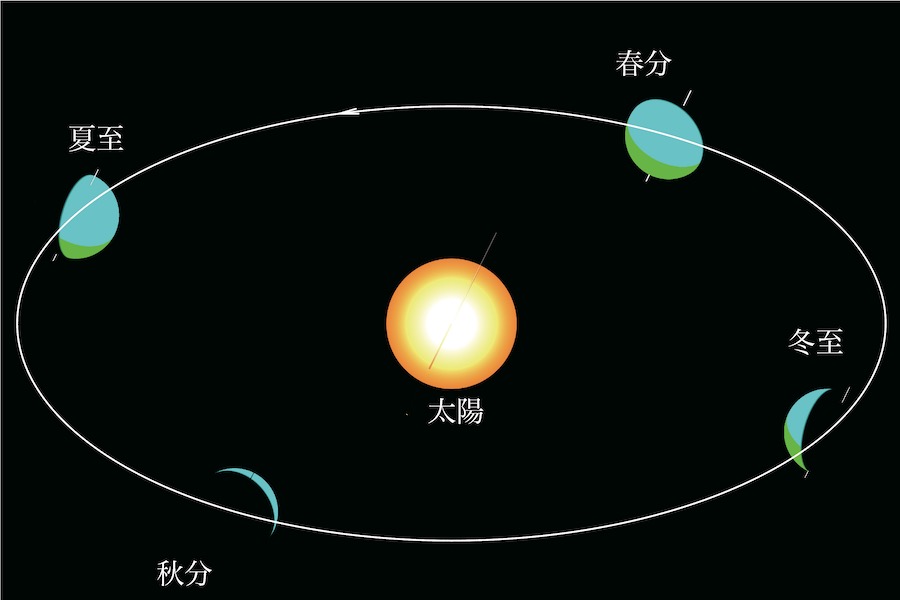

ちょっと異なる考え方をしてみましょう。
上のCGを見ていただき、太陽に注目してください。
太陽に
変な棒がささっている感じだけど・・・
これは、「地球の地軸」と全く同じ向きで少し軸を大きくして太陽に差したCGです。
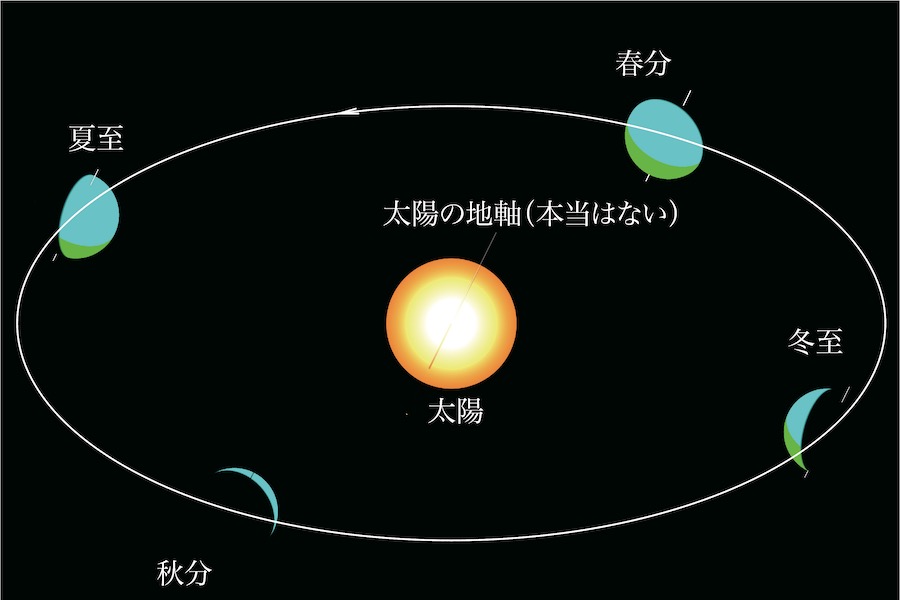

「本当はない」はずの「太陽の地軸」を勝手に僕が描きました。
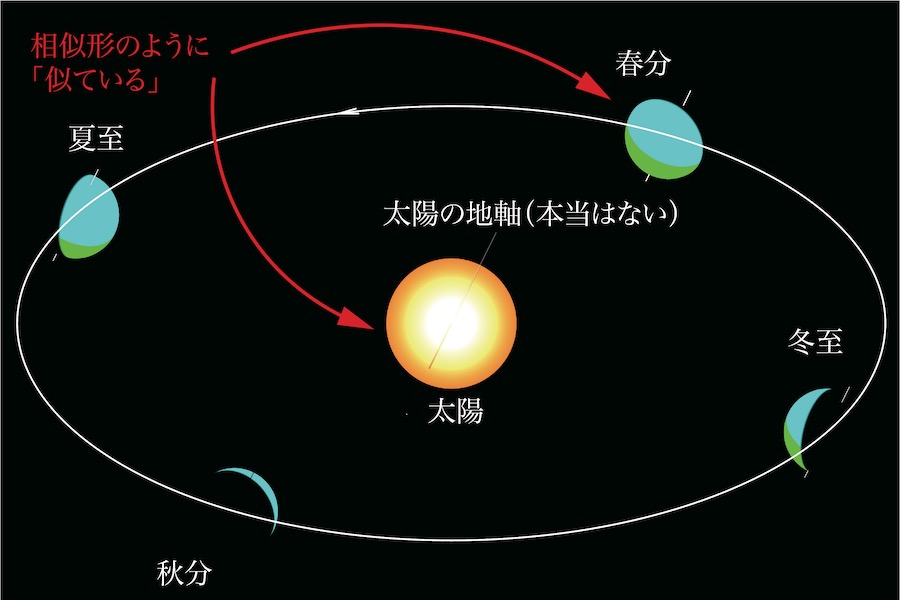

このように「余分な太陽の地軸」を付加すると、太陽と春分・秋分の地球が相似形のように似ています。
「地軸の太さ」を考慮しないと、太陽と地球が完全な球体であれば、立体の相似形になります。
地軸を含めた地球をグーっと拡大すると、「地軸がある(本当はない)太陽」になります。



確かにこう考えると、
春分と秋分の地球と太陽光の関係が分かるかも・・・



でも、ないはずの「太陽の地軸」を
勝手に加えるのは、ちょっと変じゃない?
この「ないはずの太陽の地軸」を勝手に加えることには、少し抵抗感があります。
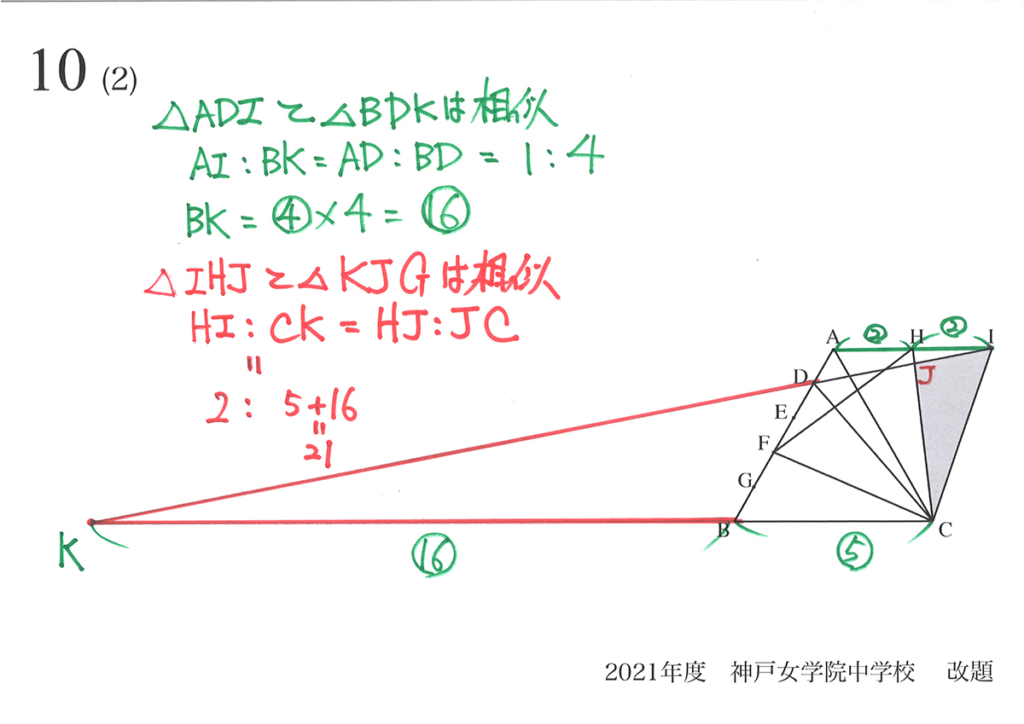

算数では補助線をひいて「ないはずの直線」を加えて考えると、解けるようになります。
天体のような「理科の現象・事実」と「算数の図形など架空の話」は全く違います。
ところが、「自分が分かるように何かを付加して考える」のは似ている面があります。
このような考え方が適切かどうかは、様々な意見があると思います。
勉強を進めてゆく上で大事なことは、「自分なりに理解する」姿勢だと思います。
上の「太陽の地軸」は少し極端な例かもしれません。
これは一例ですが、何か「自分らしく理解」するのも良いでしょう。
今回は、太陽と地球を3DCGで立体的に考えてみました。
このように天体や自転・公転を「しっかり理解する」姿勢を持てば、全て解けるようになるでしょう。
次回は下記リンクです。


