かっ車の考え方・コツ・ポイント 2〜斜めの定かっ車・力を矢印で描く・かっ車の組み合わせ・複雑な問題＝基本問題の組み合わせ・基本的考え方を身につける学び〜｜中学受験・理科

前回は「かっ車の考え方・コツ・ポイント 1〜定かっ車・力を矢印で描いてイメージ・移動距離を描いて理解・描いて理解する理科〜」の話でした。

かっ車の組み合わせ：複雑な問題＝基本問題の組み合わせ

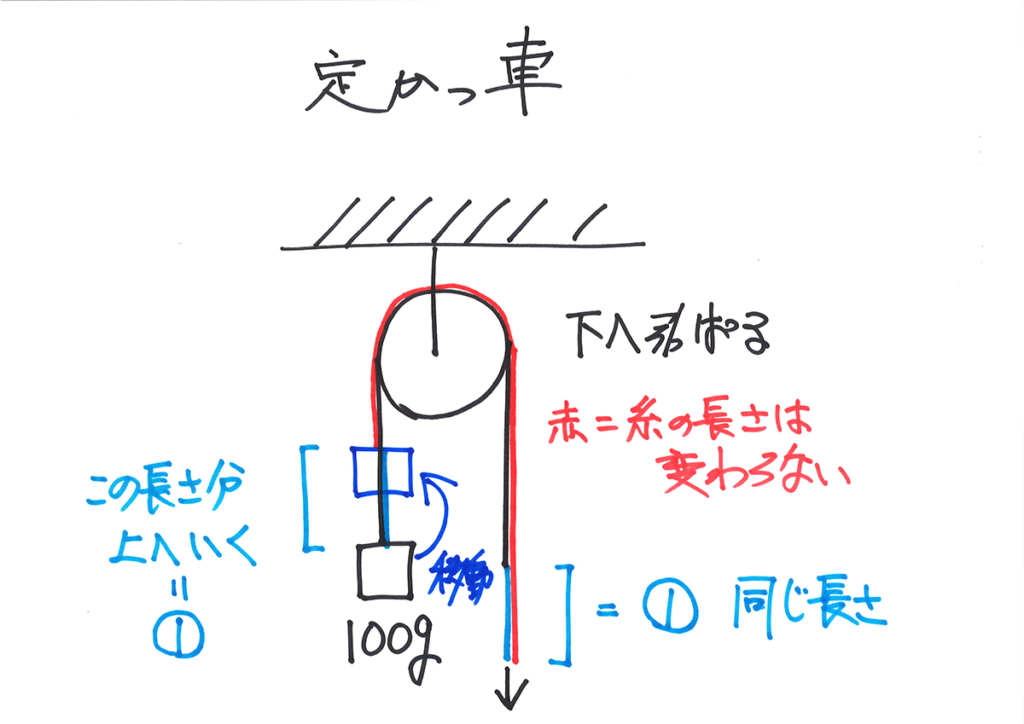
前回は定かっ車の力と動く距離・長さを考えましたが、なかなか難しいのが「かっ車」の問題です。

動かっ車と定かっ車が、いくつか組み合わさった問題もたくさんあります。

かっ車がたくさんあると、「かっ車がどう動いて、どこにどう力がかかるか」が分かりにくいです。

力や電気の複雑な問題は、基本をしっかり押さえて、少しずつ考えるようにしましょう。

そうすれば、必ず出来るようになります。

力や電気の基本的な問題は出来るようになっても、多くの人は、

応用問題は「なかなか出来ない」ことがあります。

最難関校の入試問題などで、

大人でも「理解するのが、ちょっと大変」な複雑な問題が出題されることがあります。

よく言われますが、中学入試の問題は「大人・大学生でも解けない」問題が多いです。

ある程度は、「小学校の学習内容に準拠しなければならない」中学入試。

そのため「制限された範囲で、難しくする」には、「複雑な問題になる」傾向が強いです。

算数・社会も同様ですが、「複雑な・難しい問題＝基本問題の組み合わせ」です。

そこで、複雑な問題は、絡まった糸を解きほぐすように一つ一つ考えてゆくようにしましょう。

「描いて、イメージして」基本を理解しましょう。

斜めの定かっ車：力を矢印で描く

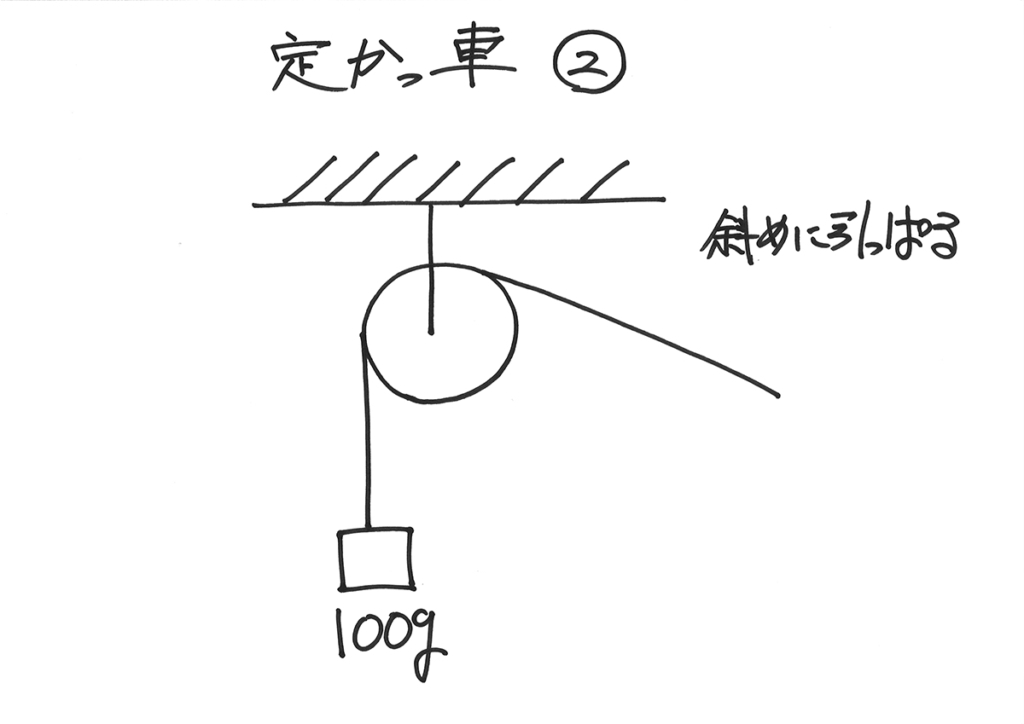
今回は、前回の「定かっ車」を、斜めから引っ張りましょう。

前回と、どのように状況が変わるでしょうか。

これは「複雑な問題」ではなく「基本」ですが、「状況が変わる」ことをイメージしましょう。

前回同様に、矢印を描いて、しっかり理解しましょう。

「100gのおもり」には、重力で下向きに「重さ」がかかりますから、矢印を描きましょう。

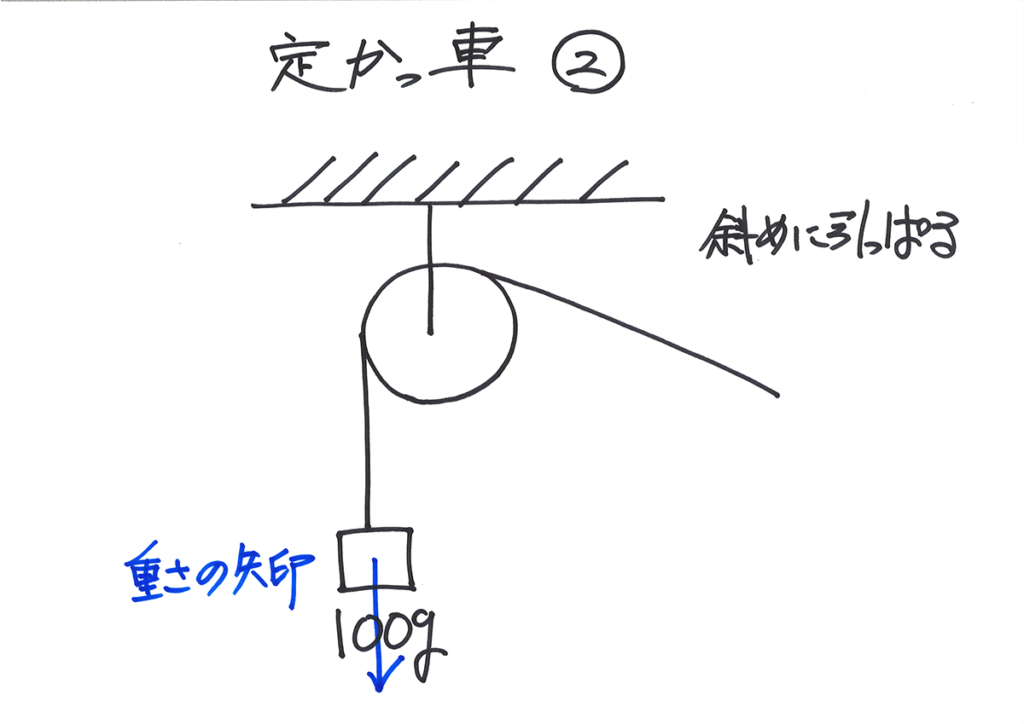
まずは、斜めに引っ張る時の「必要な力」を考えましょう。

まずは、おもりの重さ（重力）がかかり、糸の両側を考えてみます。

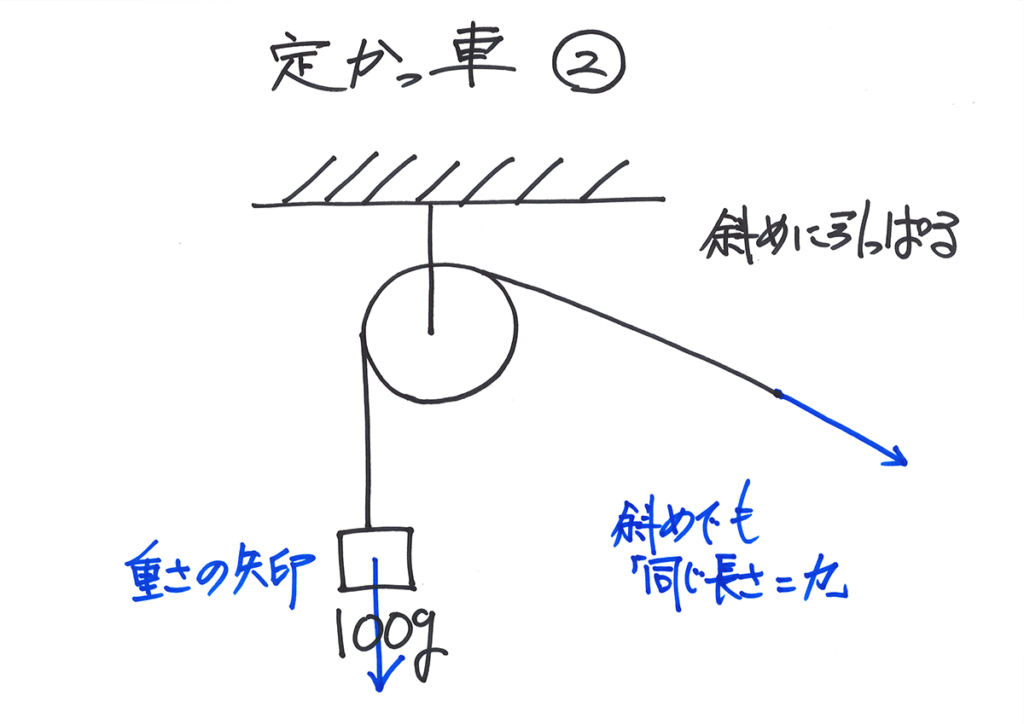
左側の端には「100gの重さ」がかかり右端を引っ張るので、「同じ長さ=同じ力」になります。

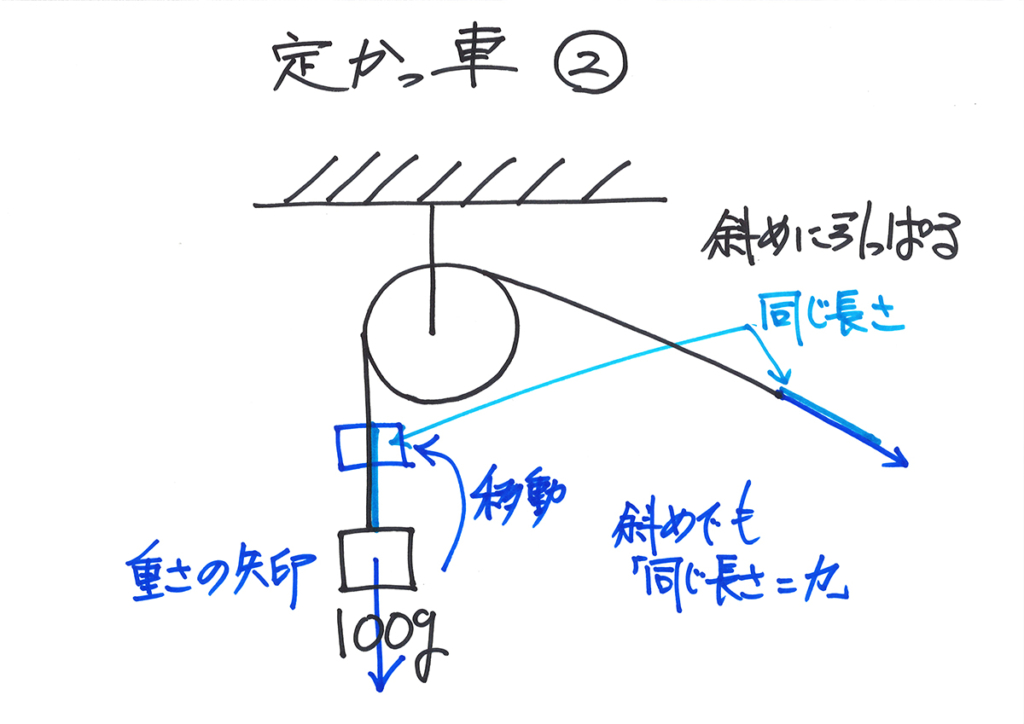
次は、引っ張る長さを考えてみましょう。

前回同様に、「おもりが移動する」状況を描いてみましょう。

糸全体の長さは変わらないので、「移動する距離=水色の長さ」と「引く長さ」は同じになるはずです。

基本的考え方を身につける学び

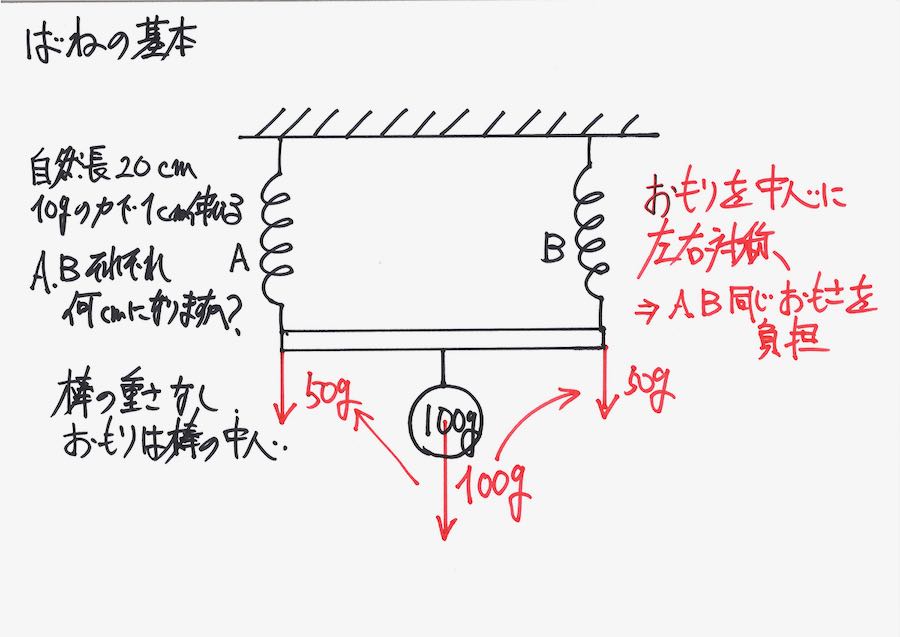
理科の生物分野は、「暗記」が多いです。

力・電気・ばねなどの力学は「この場合はこう」と丸暗記せず、基本的な考えをしっかり押さえましょう。

「問題ごとに基本に戻って考える」姿勢がしっかり身につけば、全て出来るようになるでしょう。

確かに「時間制限のある試験」では、「効率も大事」です。

こうした「基本的考え」をしっかり理解できていると、様々な応用問題に対する力もアップします。

理科の実験問題を解くコツを、上記リンクでご紹介しています。

理科の実験問題では、「基本的な考え方ができているか」が問われます。

力・電気・ばねなどの力学分野を、「鉄則」や「パターン」で学ぶ方もいらっしゃるでしょう。

問題をパターン分類・暗記した時、ある程度学力は上がります。

ただし、応用問題に対する力は「伸びにくくなる」傾向があります。

日本の中学受験〜大学受験の「単なるペーパー試験」による受験が「時代遅れ」であること。

それは、多くの学校の教員の方達は十分に理解しています。

その中で、

こう考えている出題者・教員が多いでしょう。

そういう「考え方・理解力を問う」問題が増えてゆくと考えます。

「基本的考え」をしっかり習得する勉強法は、こうした「新しい流れ」にも応じられるでしょう。

「鉄則」や「パターン」で学ぶデメリットが他にもあります。

そういう「鉄則」や「パターン」で学ぶ姿勢が身につけて中学受験は突破できるかもしれません。

ところが、中学以降に弊害が出ることがあります。

その後の「中高での学び・大学受験」において、理解力が下がる可能性が高いです。

「しっかり考える姿勢」を身につけて、学力もしっかり上げましょう。

次回は「動かっ車」を考えてみましょう。（下記リンク）