算数の学力アップ・比を具体的な量にする考え方〜意外と曖昧な比・算数で超頻出の比・図形も食塩水も登場する比〜｜中学受験・算数・比の考え方1

前回は「比の問題を解くコツ〜自分の都合が良いように問題を考える・問題のシーンを具体的に描く・「抽象的な比」を「具体的な数値」にして立式〜」の話でした。

算数で超頻出の比：図形も食塩水も登場する比

25Speed201ts

CさんがAさん、Bさんに追いつく速さの問題を考えました。

この問題では、「まずAに追いつく時間：そのあとBに追いつく時間=１：６」が条件です。

ここで、A,B,Cが「動き続けている」ので、少し難しいです。

25Speed206ts

ここで、「追いつく時間を考える起点を統一する」のがポイントでした。

今回は、算数で頻出の比に関して考えてみます。

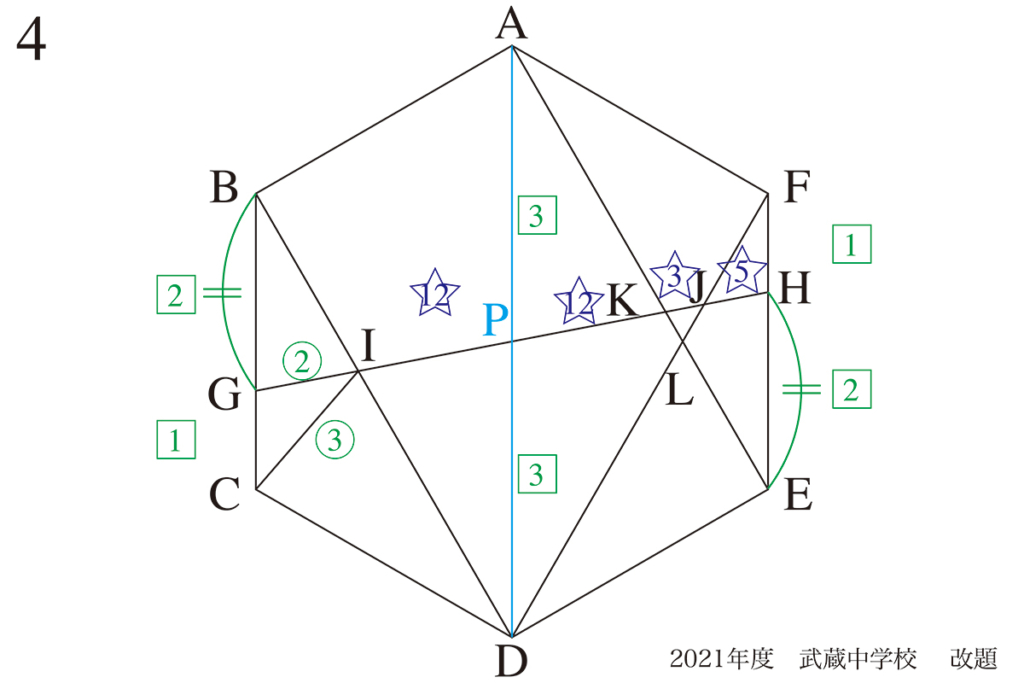
図形問題において、比は頻出であり、「面積比や辺の比が登場しない図形問題」は極めて少数です。

上の図形問題の考え方を、上記リンクでご紹介しています。

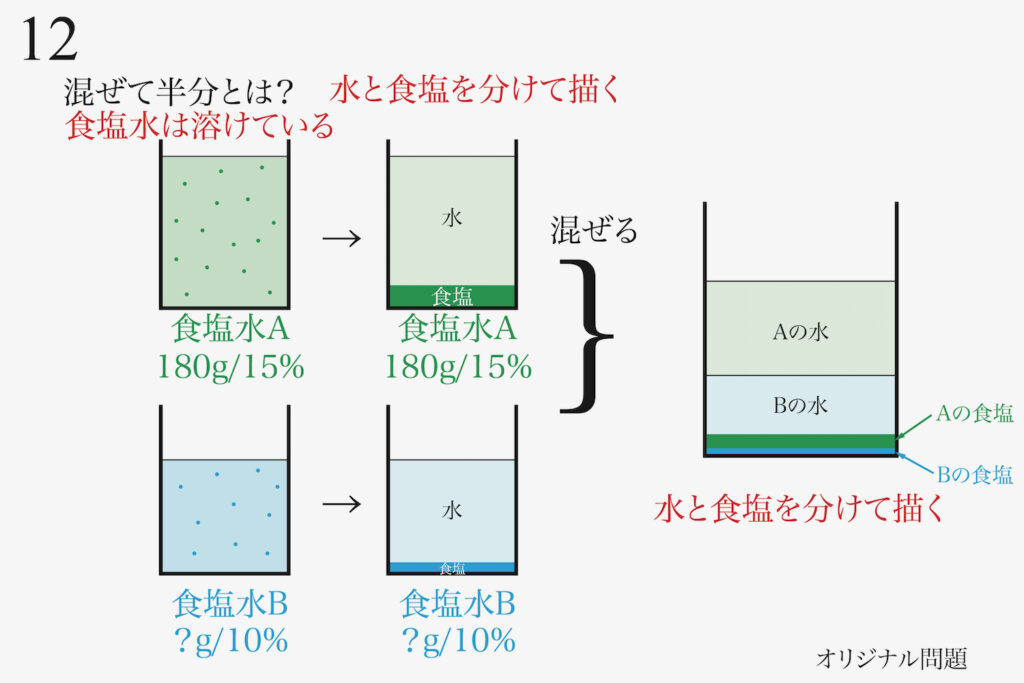
食塩水の問題では、「食塩の割合=%」が根幹です。

この「%という割合」は、「水と食塩の比」でもあります。

「3つのてんびん算」「混ぜて半分」の食塩水の問題の考え方を、上記リンクでご紹介しています。

算数の学力アップ・比を具体的な量にする考え方：意外と曖昧な比

25Speed01ts

とにかく、頻繁に登場するのが比です。

上の問題文で、「６倍」と「６：１」は同じ意味です。

その一方で、「６倍」から「６：１」と考える視点は非常に大事です。

25Ratio101ts

この問題を解く際に、鍵となったのは「時間の比」を「具体的な時間」に置き換えた点です。

25Ratio102ts

この◯や△などを使用して、「比を未知数で置き換える」発想の根幹は代数です。

小学生の皆さんが中学生になって最初に「中学らしい学び」と感じるのが、方程式です。

「算数」が「数学」に名称が変わり、X,Yが登場し、さらにZやθなどが登場します。

そして、いかにも「学問っぽくなる」印象が強いのが、これらの文字たちです。

最近の中学受験算数の教材を見ると、X,Yが使用されている教材もありましたが、

「小学生から方程式を学ぶ」考え方もありますが、一般的には、「小学生らしい学び」が望ましいです。

XやYが登場した時に、

このように理解する小学生は少数派であり、学力が高めの小学生であっても、

このように「難しい」と感じるほうが正常な反応です。

そこで、小学生が理解しやすいように「XやYの代わりに◯や△を使う」のが算数です。

これは「ただ見かけが変わっただけ」で、「考え方は同じ」です。

その一方で、「見かけが変わる」ことは大事です。

こうして、◯や△を設定して問題を解くことが多いです。

ここで、「◯や△の未知数設定」を「解く定石の一つ」と考えない視点が大事です。

「定石」や「典型」でも良いですが、ここで「◯や△の未知数設定」は「分からない数値を設定」です。

この考え方は、数学的であり大事ですが、ここで「算数的発想」で考えてみましょう。

上の問題では「時間の比を◯で置いた」解き方です。

25Ratio103ts

ここで、「未知数設定」ではなく、「曖昧な比」を「具体的な数量」にしたと考えてみましょう。

比は「分かりやすい様で分かりにくい」です。

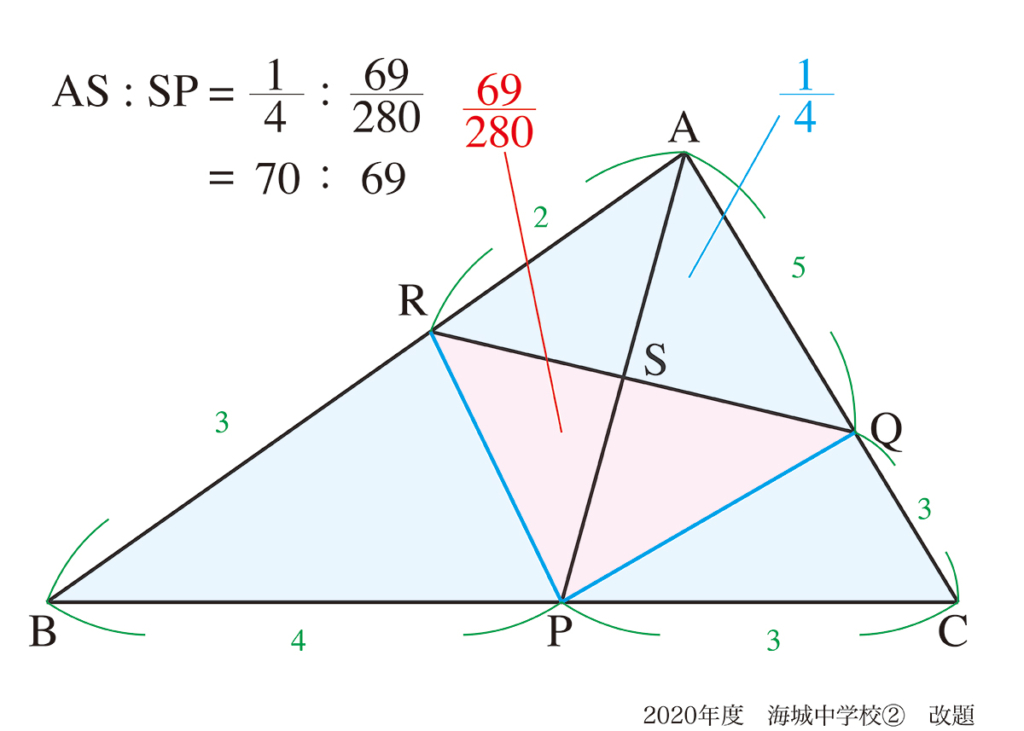
図形問題では、「具体的な図形の大きさや辺の長さ」が目前にあるので、面積比や辺の比が分かりやすいです。

その一方で、「時間の比」や「何かと何かの比」は、曖昧でモヤモヤした感じです。

そこで、「◯や△の量（時間）」にすると、具体的になって分かりやすくなります。

この「具体的な数量に置き直す」視点で考えると、算数の考え方が広がり学力がアップするでしょう。