前回は「入試が難しい時→「自分は有利」と思って合格へ〜「全能力+脳力」を試験へ・東郷平八郎「勝利確実」の強い思い・「禁じ手」だった東郷ターン〜」の話でした。
天候も気持ちも朗らかにして合格へ
本日は、2026年1月31日となり、いよいよ明日2月1日から首都圏の中学受験が本格化します。
筆者は、36年前、1990年に中学受験をしました。
1/3世紀以上昔のことであり、現在の中学受験とは異なる点も、同じ点もあります。
1990年2月1日は首都圏で大雪が降り、入試当日は電車のダイヤが乱れ、大変な状況でした。
大雪の中、入試の試験場である志望校に向かったことを、今でも覚えています。
明日は首都圏は天気が良さそうで、まさに「天候晴朗なれども」となりそうです。
気持ち晴朗に合格に向かう話を、上記リンクでご紹介しています。
天候も気持ちも朗らかにして、試験場に向かって、合格に進む気持ちが大事です。
難問の効果的考え方「簡単な特定の場合」設定：落ち着いて描く
中学受験から大学受験で、最も点差が付きやすい科目である算数・数学。
後から解答を読めば、
女子小学生こう考えたら、
簡単だったんだ・・・
こういうことが良くあり、他の科目にはない「微妙な悔しさ」があるのが算数・数学です。
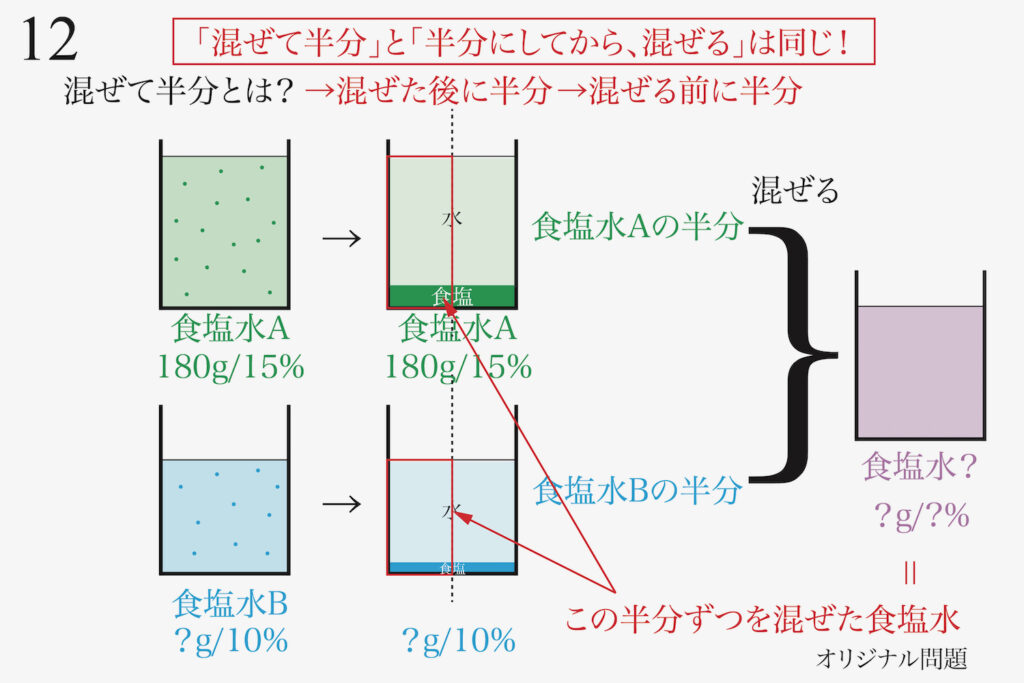
上記リンクでは、「食塩水を混ぜて半分」を描いて、理解する話をご紹介しています。
このように、算数では、「描くと分かる」けど「描かないと、なかなか分からない」ことがあります。
男子小学生これは
どういうことだろう・・・
最近は、複雑な「初見の問題」が増えているように感じます。
シンプルな「初見な問題」を作成するのは、極めて困難であるので、
出題者出来るだけ、
類題がない問題を・・・
「類題が少ない」「パターン化してない」問題を作成すると、複雑になる傾向があります。
こういう時は、多くの場合で、
出題者難しいので、（１）は
特定の場合を考えて下さい・・・
出題者例えば、Aが５の場合は、
どうなりますか？
このように、（１）で特定の場合を考える、比較的易しい問題があることが多いです。
その一方で、このような「特定の場合の出題がない」場合もあります。
男子小学生よく分からない・・・
どう解けば良いのかな・・・
場合の数の問題で、「設定がされていない条件」がある問題も見かけます。
ここでは「ゼッケンをつける」考え方を、上記リンクでご紹介しています。
これらの「よく分からない」問題の時は、「特定の場合」を考えてみると分かることが多いです。
例えば、速さの問題だったら、「丁度半分の中間地点で出会ったら、どうか」など。
動く点の問題は、「状況を把握する」ことが大事ですが、「一つの例を考える」など。
難しい問題は、自分で「仮にこういうことなら、どうなるか？」を考えると、分かりやすいです。
そして、その「自分が設定する状況」は、出来るだけ簡単で、暗算できる位、が良いです。
女子小学生この速さの問題は、
AくんとBさんが出会って・・・
女子小学生比がポイントのはずだけど、
速さの比？時間の比？
女子小学生もし、真ん中で
出会ったら、こうなるね・・・
女子小学生あっ、そうか・・・
こう考えたら、良さそう・・・
問題に対しては、自分の都合良いように考える姿勢も大事です。
次の問題文を読んでみる考え方
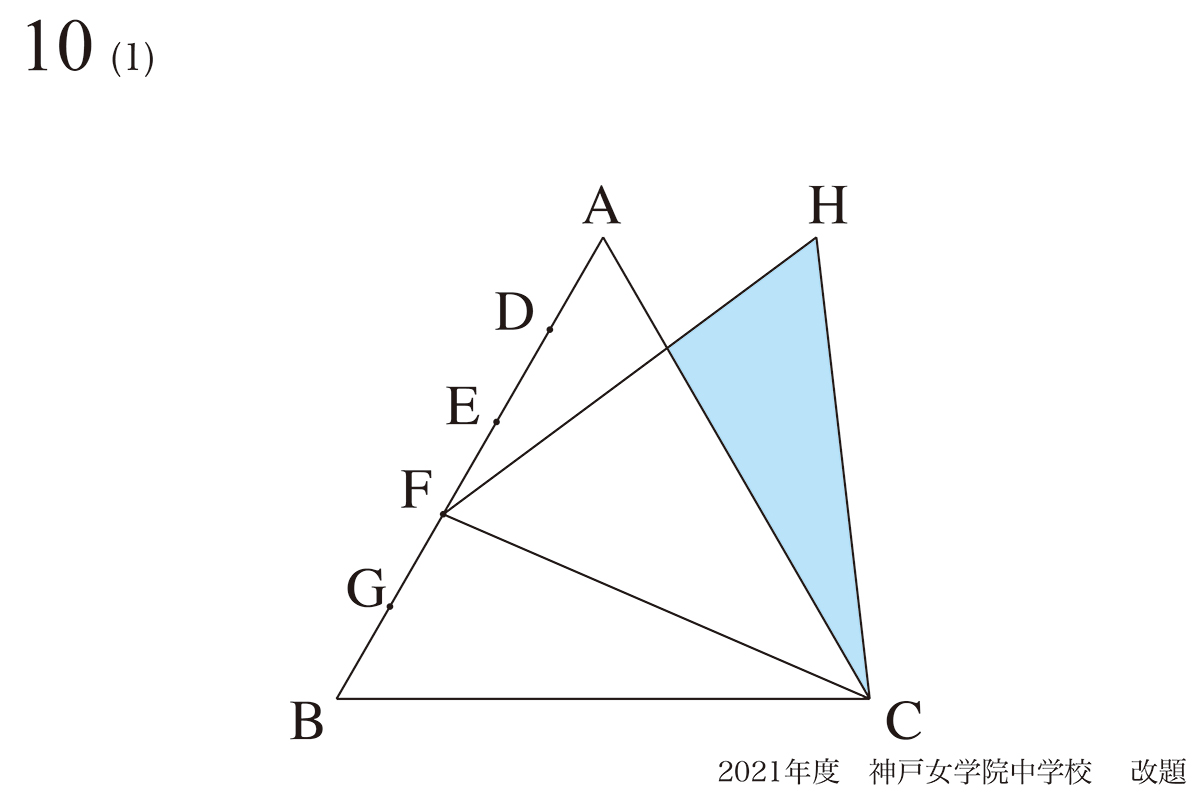
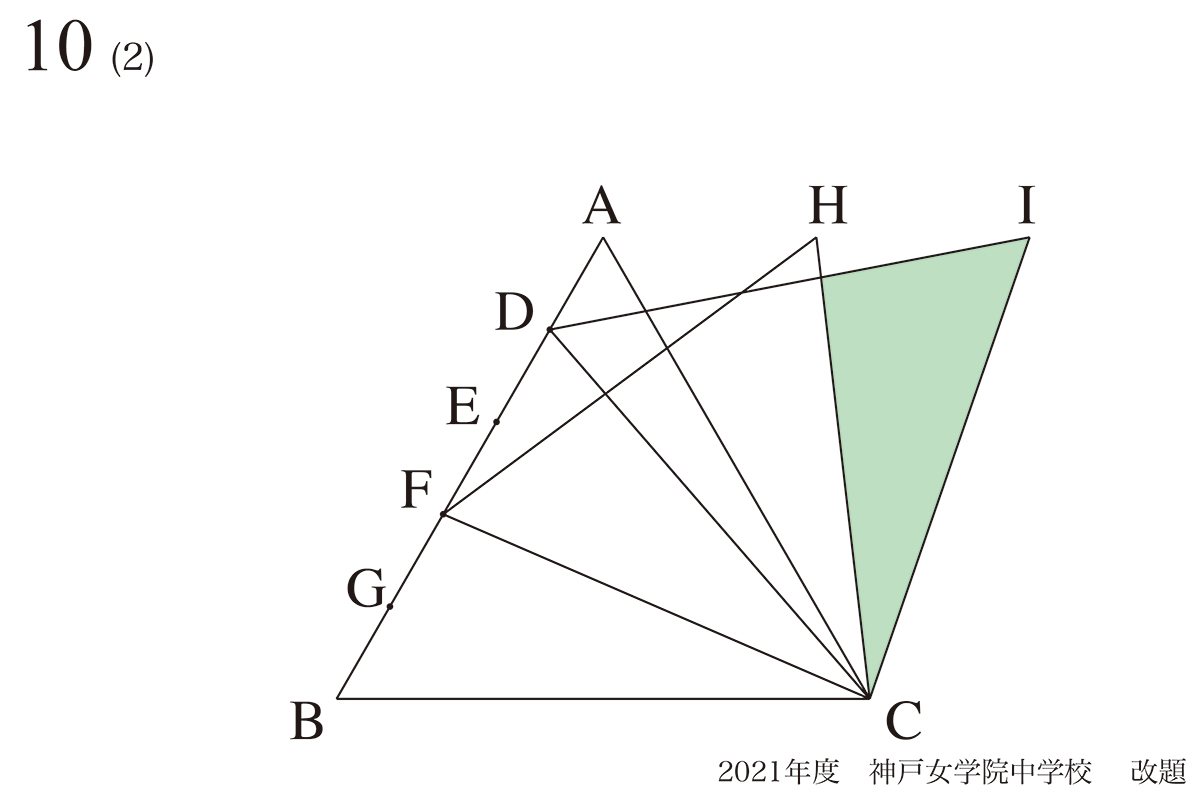
算数では、（１）（２）・・・と小問がある大問があります。
難関校、最難関校、などは、大問が多い傾向があります。
こういう問題を解く時は、
男子小学生よしっ、
まずは（１）！
「まずは（１）から」と考えることが多く、「先の問題は読まない」ことが多いです。
スラスラ行けば良いですが、
男子小学生？？？
よく分からない・・・
よく分からない時は、先の問題を読んでみましょう。
男子小学生（２）はどんな問題？
（３）は？
大問は、「前の問題がヒント」であることが多いです。
そして、「同じ内容を対象とした問題」であるので、共通点があります。
すると、先の問題を読むと、ヒントが得られる可能性があります。
「前の問題がヒント」であることが多いですが、「後ろの問題がヒント」の場合もあります。
上の図形問題では、「正三角形が回転」という「似ている状況」であり、
男子小学生なんか、
似ているな・・・
男子小学生あ、
ひょっとして・・・
このように、「先を読む」ことで「問題の大事なポイント」がつかめることもあります。
「正三角形の回転」の問題の考え方を、上記リンクでご紹介しています。
・特定の、簡単な場合を設定する
・先の問題文を読む
このように、算数は「全体を見る」姿勢で考えると、解きやすいことがあります。
明日以降、受験生の皆さんは全力を出し切るように、試験に臨むことを願っています。
まずは体調第一で、健康に、朗らかに、冷静に。
中学受験生・高校受験生・大学受験生の皆さんの志望校合格を、心より祈念しています。
