図形問題が解けるようになる勉強法〜たくさんの公式が登場する算数・相似比と面積比を説明・「分からない」と手を止めないで手を動かす〜｜2025算数の学び1・中学受験

前回は「「算数が苦手」な人が解けるようになる勉強法〜「描いて理解」か「すぐに立式」の二つだけ・状況把握して的確に立式・「式を立てる」ことを強く意識〜」の話でした。

たくさんの公式が登場する算数

ms18_01ts

以前、上記のような「正三角形が二つ」ある図形問題を考えました。

この問題の考え方は、上記リンクでご紹介しています。

この問題は1984年に武蔵中学で出題された問題で、現在2025年から考えると40年以上前です。

「40年前」は小学生〜高校生にとっては、「大昔」で想像するのが難しい面があると思います。

一方で、「40年前」はそれほど昔ではなく、筆者は小学校2年生でした。

筆者と同世代の方も、同じように感じると思います。

1985年の雑誌「週刊朝日」の大学進学実績特集号の話を、上記リンクでご紹介しました。

40年も前の過去問は、手に入れるのが大変困難ですが、この頃も良い問題が多数あります。

上の問題を「初めて見る」方は、ぜひ解いてみて頂きたいと思います。

この問題の一つの特徴は、「相似比1 : aの図形の面積比は1 : a x a」であることを説明していることです。

算数や数学では、多数の公式が登場します。

「どこまで公式として考えるか」に対しては、様々な意見があります。

このように考える人もいれば、

「公式よりも理解が大事」という考え方の人もいます。

筆者は、後者の「一つ一つきちんと理解する」考え方が良いと考えます。

制限時間があるテストにおいては、公式をたくさん知っている方が得点が上がる傾向があります。

一方で、応用問題が多いテストでは、「公式のみ」では解けない場合が多いです。

この「公式をたくさん」と「理解中心」に関しては、受験する学校の出題傾向にもよります。

数多くの問題が出題される場合は、「公式をたくさん」も良い面があると思います。

「公式を暗記」と考えると、沢山ありすぎて大変な面があります。

「分からない」と手を止めないで手を動かす

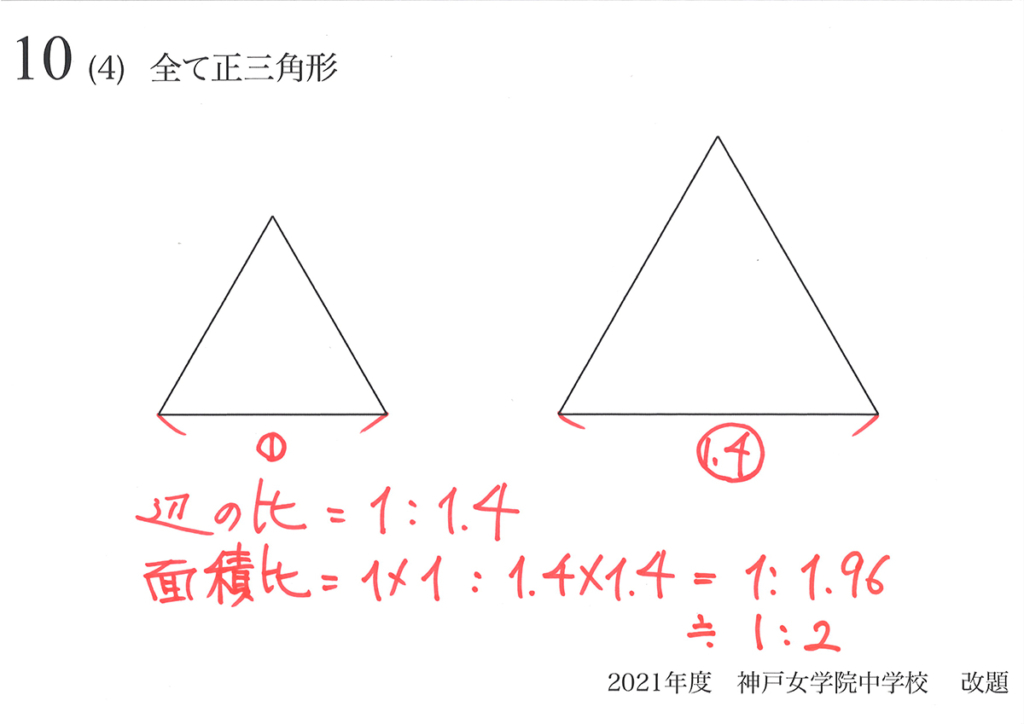
それでは、「相似比1 : aの図形の面積比は1 : a x a」を説明出来るか、考えてみましょう。

公式は「説明出来る」のが望ましく、説明出来る方が算数の学力が大きく上がります。

確かに、公式を使って「ズバッと解ける」問題もあります。

一方で、「公式のみでは解けない」応用問題もたくさんあります。

筆者は「公式を説明出来る学び」をすることをお勧めします。

「公式を説明出来る」と、公式をしっかり理解することになり、応用力が格段に上がります。

特に、図形問題では、多数の公式や性質が登場しますが、それらをしっかり理解してみましょう。

すると、図形問題が解けるようになるでしょう。

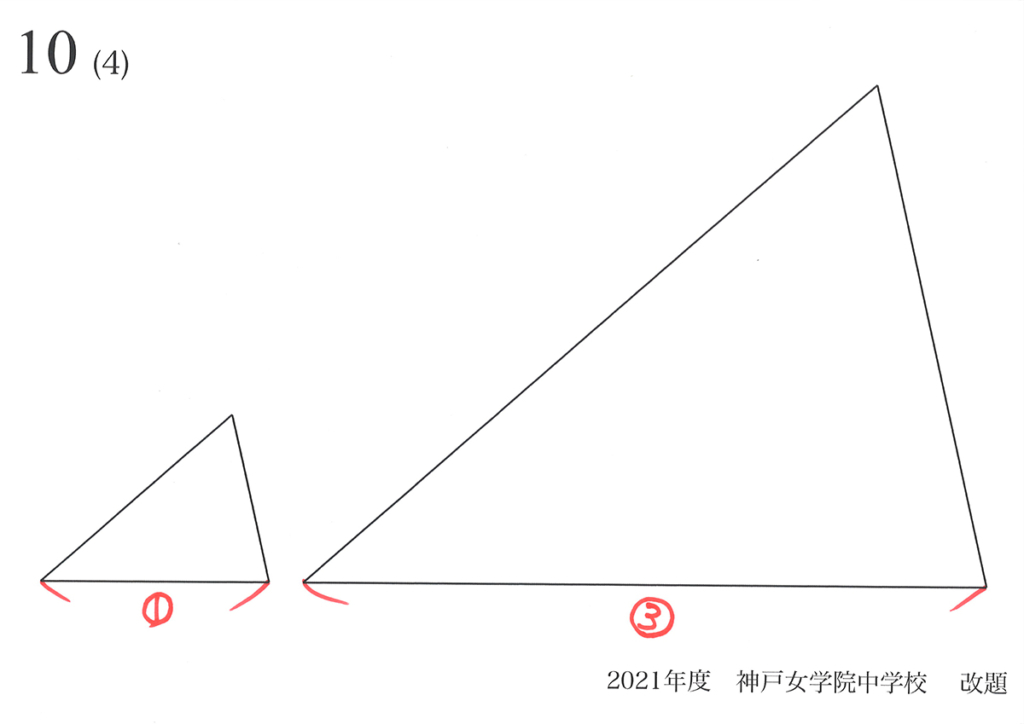
上の二つの相似形において、「相似比１：３の相似形の面積比は１：９」となります。

この「面積比１：９」を説明することを考えてみましょう。

「直感的に」では説明にはなりませんが、「直感」は算数や数学では大事にしましょう。

「分からない」時は、手が止まってしまいますが、手を動かすようにしてみましょう。

図形問題が解けるようになる勉強法：相似比と面積比を説明

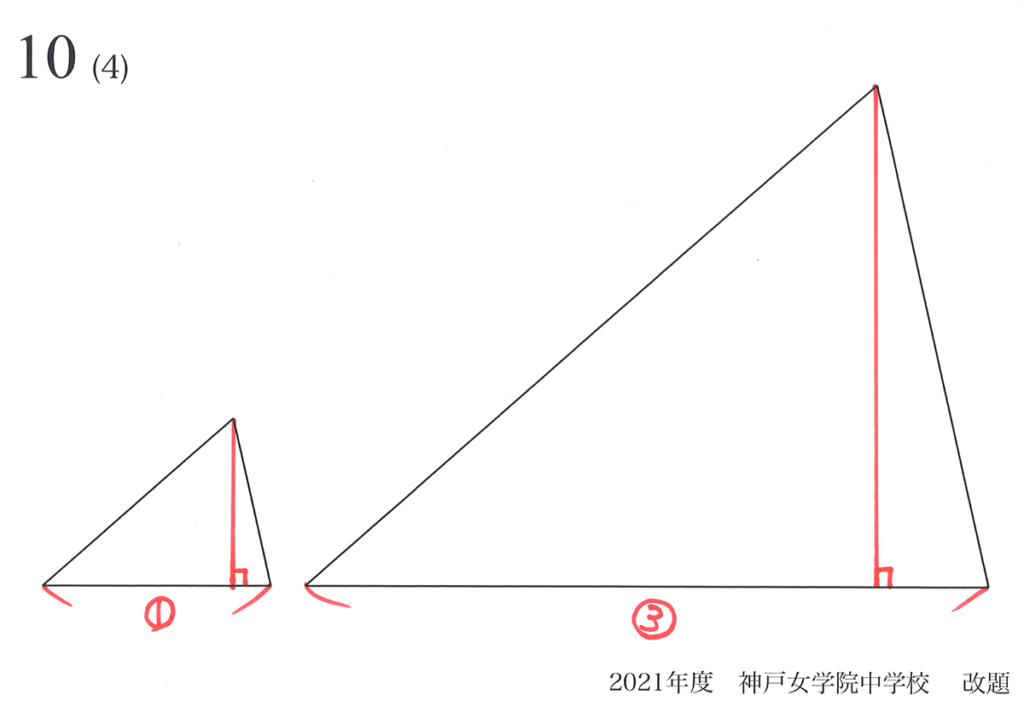
二つの三角形の面積比を考えていますが、「面積の計算の仕方」をもう一度考えてみましょう。

「三角形の面積=底辺x高さ➗２」は、超基本なので、しっかり理解したいです。

この「三角形の面積=底辺x高さ➗２」は、図形の基本というよりも「決まり事」とも言えます。

そこで、「三角形の面積=底辺x高さ➗２」は、公式というよりも「決まり事=前提」で良いでしょう。

分数を習った後は「三角形の面積=底辺x高さ➗２」ではなく「三角形の面積=底辺x高さx1/2」が良いです。

「➗２」と「x1/2」は、算数・数学的には同等ですが、意味が少し異なります。

相似比などを考えるときは、比や比率を考えます。

そこで、三角形の面積の計算の際も、掛け算の方が統一感があって分かりやすいと思います。

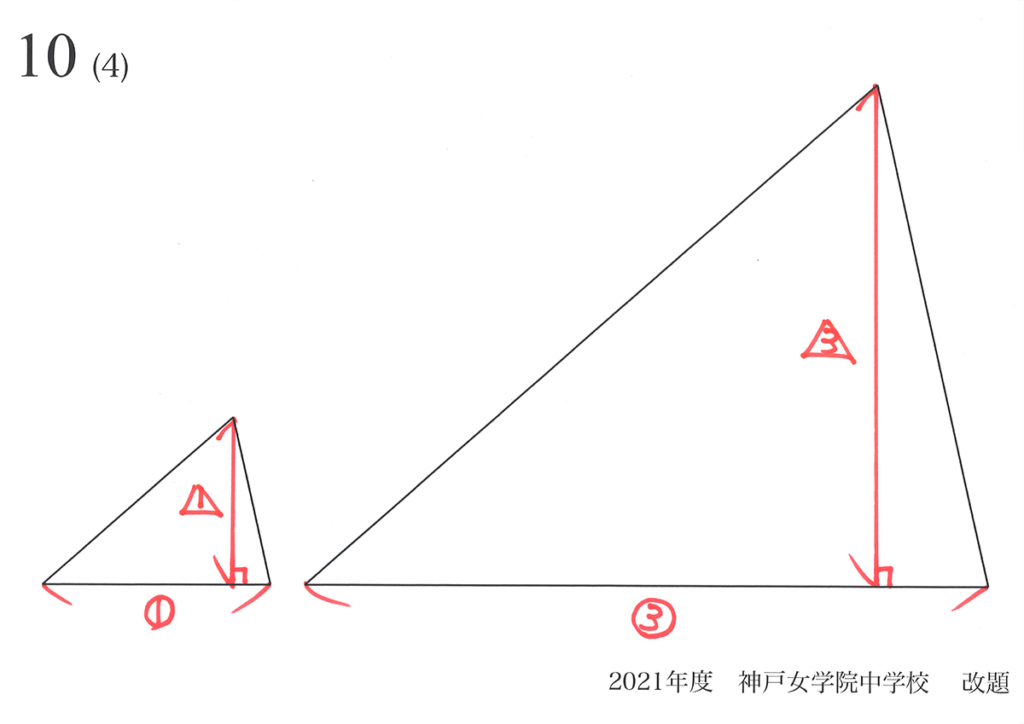
「相似比が１：３」ということは、「相似の部分は全て１：３」です。

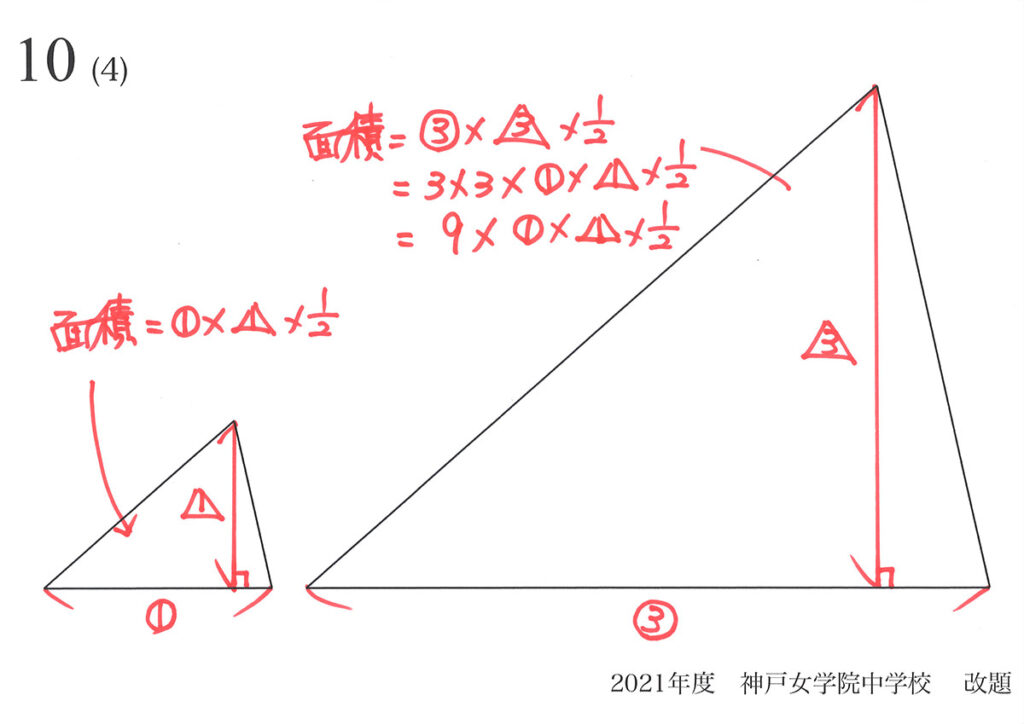
両方の三角形の面積を計算すると、きちんと「面積比１：９」が分かりました。

このように、図形の様々な公式や性質をもう一度復習すると、様々な図形の大事なことが分かります。

すると、特に図形の応用問題が解けるようになるでしょう。