前回は「算数の総合力を上げる勉強法〜色々な角度から考える・図形問題の「思考の軸」・比とは「比較する」こと・複雑な形と単純な形・合体と分解〜」の話でした。
難問を解く学力を上げるポイント:「遠回りな勉強」で鍛えられる応用力
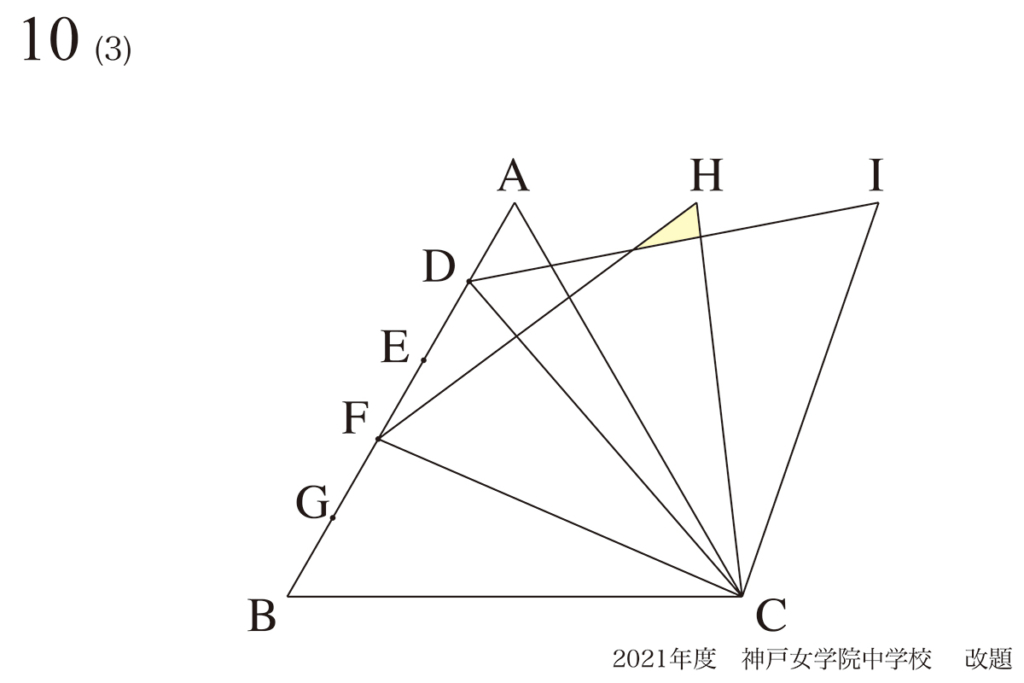
図形問題では「解答とは異なる補助線でも考えてみる」ことが大事です。
解答に載ってないと、
「違う補助線が良いかどうか」分からないよ。
これでいいのかしら、と
思ってしまうけど・・・
「正しい答え」に対して点数が与えられ、「誤まった答え」に対してはX(バツ)か大幅減点となる試験。
受験生は「正しい答え」を求め続けて、一生懸命勉強します。
すると、「問題集や参考書に記載されている考え方=正しい答え」のみが正しいと考えてしまいます。
算数では問題の考え方は複数あることが多く、図形問題は「解ける補助線」がいくつかあることがあります。
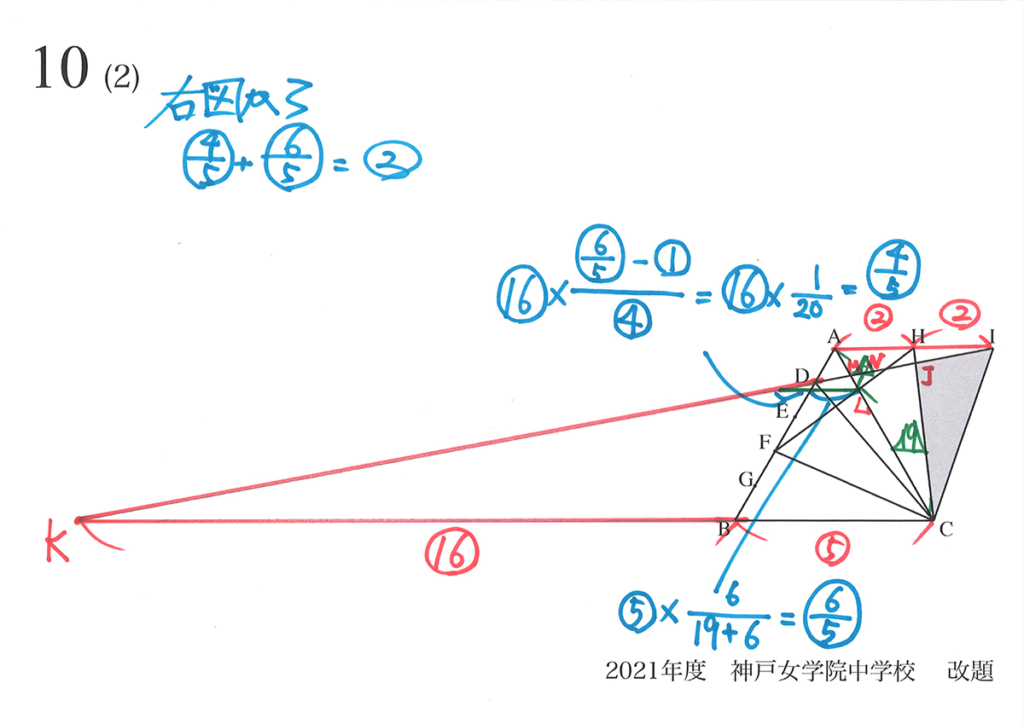
答えと違うけど、
この補助線は、良いのかな?
私はこう引いてみたけど、
どうなのかな?
自分で考えてみた補助線があれば、塾や家庭教師の先生に聞いてみるのが良いでしょう。
聞いてみる方がいない場合は、
答えがあっているから、
この考え方もOKなはず!
くらいな気持ちで良いでしょう。
高校数学になると「大体の方向性は合っているけど、論理の飛躍(ギャップ)がある」ことがあります。
この「論理のギャップ」は大事なポイントで、ある場合はX(バツ)かXに近い評価になります。
これは数学的な話であり、中学受験の算数ではあまりないことです。
なんか
良さそうだから、いいかな?
「大体の方向性が合っていればOK」という姿勢が、「思考の軸」を育てるでしょう。
・分野ごとに共通する「考え方=思考の軸」を考える
・問題ごとのバリエーションの違いは「同じ」と考えられる思考力育成
面積を求める複数の視点:様々な辺の比
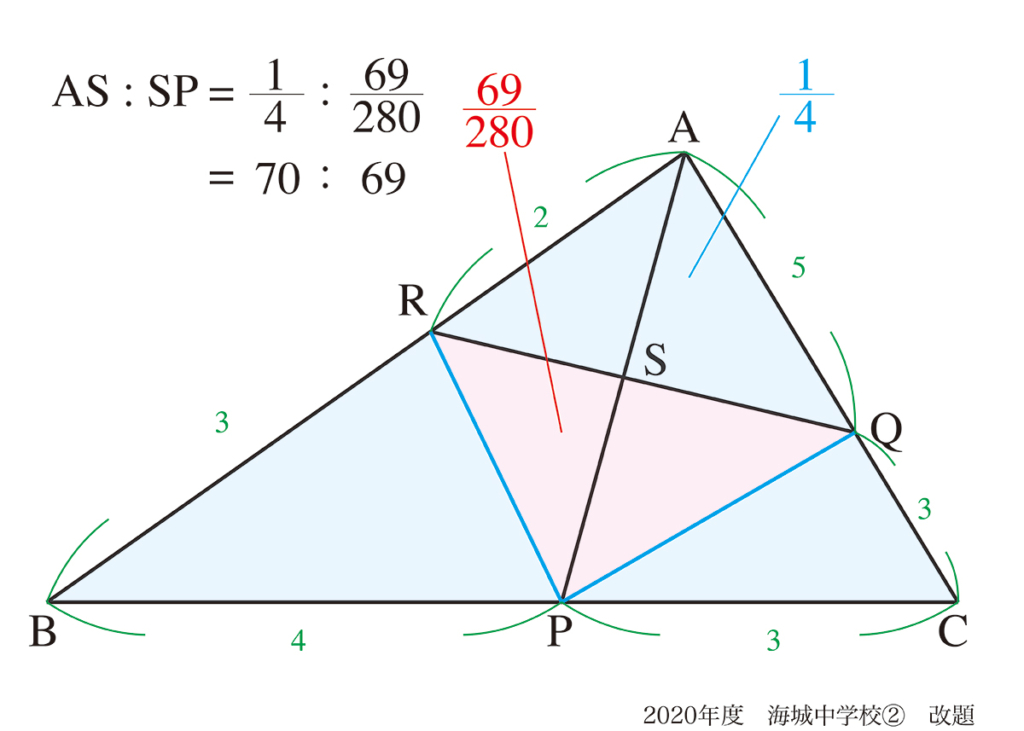
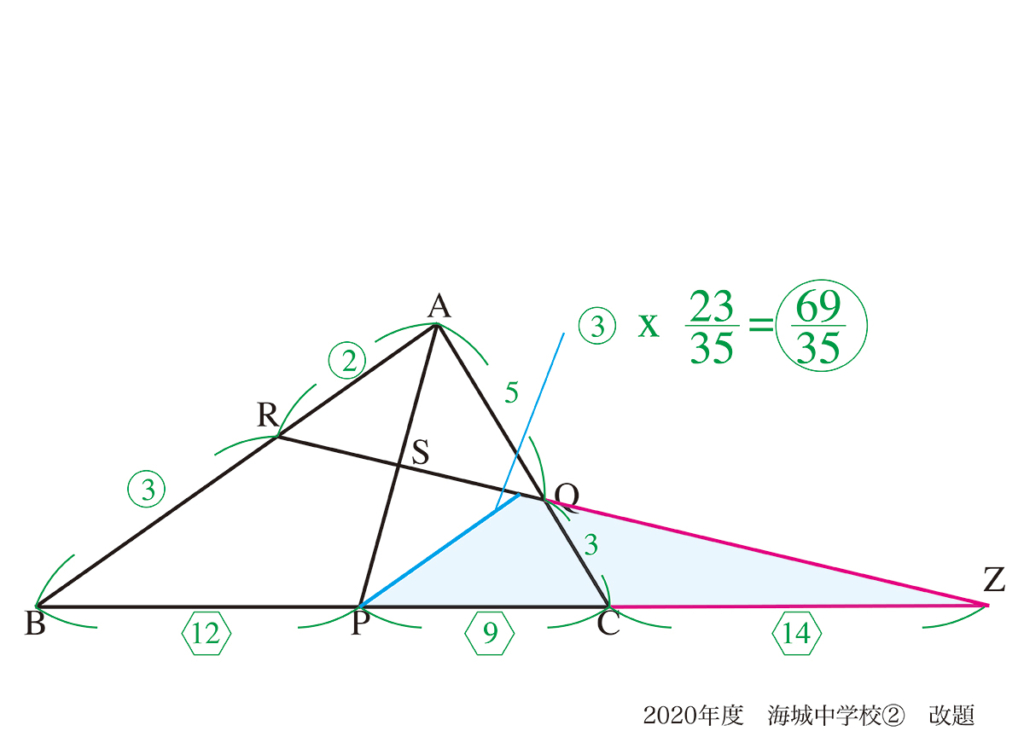
図形の面積を求める問題では、問題集や参考書では大抵「一つの方法」が紹介されています。
上の黄色の部分の面積を求める考え方を二つ紹介しました。
一つは「(1)で考えた面積から求める」で、もう一つは「(2)で考えた面積から求める」でした。
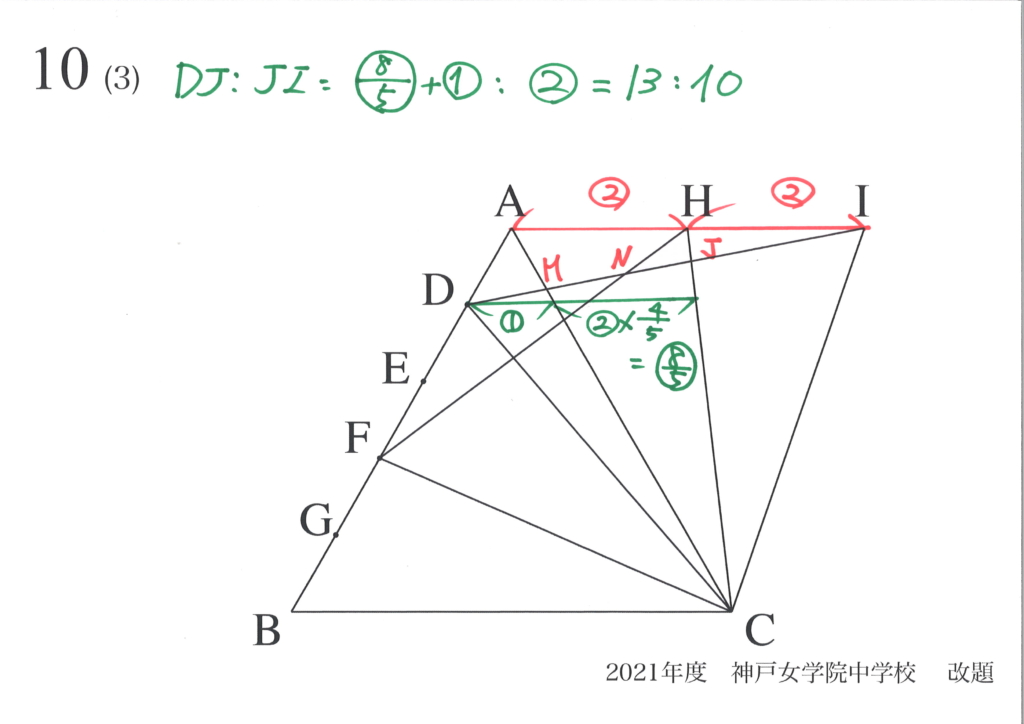
この考え方は、「両方とも正しい」考え方です。
「どちらが良いか」は、様々な方の意見があります。
・正三角形・正方形など基本的な図形が「根幹となる図形」の時は、常にその図形に注目
・「根幹となる図形」のある辺と「平行な辺」があるときは、その辺に注目
(1)から考える解法Aの方が「少し素直」です。
「少し素直」ってことは、
解法Aの方が「良い」ってこと?
これは「好み」もありますので「どちらが良いか」は、あまり考えすぎない方が良いでしょう。
「自分が好きな考え方が良い方法」くらいな考え方が良いでしょう。
・平行な線、相似形を探す・つくる
・相似比となる「対応する辺」の長さを計算
・「対応する辺の長さ」が分かりにくい時は、辺を分割して考える
算数の腕力を鍛える姿勢:少し遠回りでも解答にたどり着く
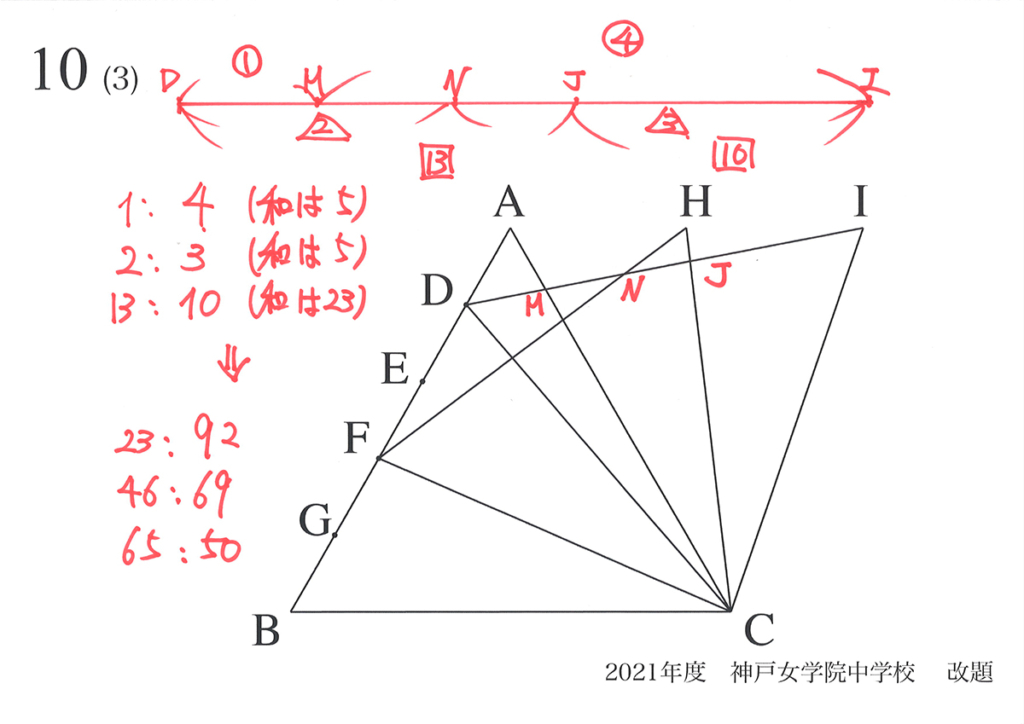
解法Bの方法は「少し遠回り」ですが、「悪い解法」とは思いません。
いずれの考え方も「相似形をしっかり把握している」意味では、しっかりできています。
きちんとした「図形的・幾何学的考え方」です。
この「相似形を考える」のは「図形問題の基本」です。
・平行な直線があると、その周辺に相似形がある
・相似形が見つからないときは、自分で相似形をつくる
「平行な直線」から、「相似形を見つけて、比を少しずつ考えてゆく」ことは大事な姿勢です。
解法Aの方が「少し素直」は、「見通しが分かりやすく、プロセスが比較的簡単」という意味です。
「見通しが良い」ことは、算数・数学では非常に大事なことです。
「見通しが良い」って
どうやったらわかるようになるの?
この感覚・勘を身につけるのは「自分で、たくさん問題を解いて図形を描いてみる」が良いでしょう。
自分で紙に書いて、しっかり解くときに、
なぜ、このような
考え方をしているのかな?
を考えながら解いてみましょう。
各分野の「基本や初歩的考え方」は「そういうもの」として習得することになります。
対して、応用力を身に付けるためには、自分で考えて試行錯誤することも大事です。
でもさ、
時間がかかるのは困るよ・・・
この「学び方」に関しては、本人の学力や個性次第です。
塾の先生や家庭教師と相談すると良いでしょう。
・解答に至らない「無駄なこと」が大事
・「遠回り」や「無駄」を経験すると、試験で「何が大事か」の感覚が磨かれる
実際にやってみると、解法AとBを想定した時、
Aの方が
少し近道だな・・・
というのが、わかるでしょう。
慣れると最後までやらなくても最初の時点で、
Aの方が
楽そうだな・・・
というのが分かるようになります。
早くそうなりたいけど、
簡単な方法はないの?
これは、「教えてもらう」よりも「自分でやってみる」と身につくことです。
時間が
かかるのかな・・・
算数はやっていると、
ああ、
こういうことかな・・・
と気づくことがあります。
「自分でやってみる」とそうした気づきに近づくので、急がない方が良いでしょう。
解法は「近道・簡単な方が良い」ですが、少し遠回りでも解答にたどり着く「算数の腕力」も大事です。
・「少し遠回りかもしれない」ときでも、解答にたどり着くパワー育成
・自分の「思考の軸」に応じて、解答にしっかり近づく姿勢
特に難関校〜最難関校を目指す方は、こういう「算数の腕力」を身に付けるように考えると良いでしょう。
これは「筋肉トレーニング」のような「思考のトレーニング」とは異なります。
計算力のような「単なる素早さ」ではなく、思考力を磨くことになり、将来にもちながるでしょう。
そのために、「しっかり図形を描いて、自分でやってみる」を実践しましょう。





